阅读:Lisp: Good News, Bad News, How to Win Big
在愁事交织的时候不由感到烦闷,就会变得无所事事,顾左而右,一天就过去了,这时候博客似乎变成了另一种集中精力的方式.这篇文章以前也是没有耳闻,一开始是来看“The Rise of Worse is Better”的,又被一个html引到了这篇文章,Google了一下竟然还是推荐必读的10篇文章之一,那么就权做解闷来阅读一下,做成翻译又怕水平不够,就当做自己的理解来写这篇翻译罢.
Lisp: Good News, Bad News, How to Win Big
Abstract
Lisp has done quite well over the last ten years: becoming nearly standardized, forming the basis of a commercial sector, achieving excellent performance, having good environments, able to deliver applications. Yet the Lisp community has failed to do as well as it could have. In this paper I look at the successes, the failures, and what to do next.
Lisp在最近十年表现的非常好:变得近乎标准化,形成了商业部门的基础,实现了优秀的性能,有一个好的环境,能够用来开发应用.然而Lisp社区却没有能够做到更好(could have).在这篇文章中我关注它的成功,失败和下一步应该怎么做.
The Lisp world is in great shape: Ten years ago there was no standard Lisp; the most standard Lisp was InterLisp, which ran on PDP-10s and Xerox Lisp machines (some said it ran on Vaxes, but I think they exaggerated); the second most standard Lisp was MacLisp, which ran only on PDP-10s, but under the three most popular operating systems for that machine; the third most standard Lisp was Portable Standard Lisp, which ran on many machines, but very few people wanted to use it; the fourth most standard Lisp was Zetalisp, which ran on two varieties of Lisp machine; and the fifth most standard Lisp was Scheme, which ran on a few different kinds of machine, but very few people wanted to use it. By today’s standards, each of these had poor or just barely acceptable performance, nonexistent or just barely satisfactory environments, nonexistent or poor integration with other languages and software, poor portability, poor acceptance, and poor commercial prospects.
Lisp世界在一个很好的环境之下:十年之前没有标准Lisp,最接近Lisp语言标准的是InterLisp,运行在PDP-10s和Xerox Lisp机器上;第二标准的Lisp是MacLisp,只能运行在PDP-10s上,但是是在这个计算机的三个最流行的操作系统上;第三标准的Lisp的是Portable Standard Lisp,它可以运行在很多机器上但是很少有人去使用它;第四标准的Lisp是Zetalisp,运行在2种Lisp机器上,第五标准的Lisp是Scheme,运行在几种不同的机器上,但是很少的人想要使用它.按照今天的标准来看它们,当中的每一个都只有勉强可以接受或是很少的特性,不存在的或是勉强可以接受的环境,不存在或是很少的和其他语言的集成,少的可怜的可移植性,认可和商业前景.
Today there is Common Lisp (CL), which runs on all major machines, all major operating systems, and virtually in every country. Common Lisp is about to be standardized by ANSI, has good performance, is surrounded with good environments, and has good integration with other languages and software.
今天我们有Common Lisp,可以运行在所有主流的机器和操作系统上,并且在几乎所有的国家(被使用).Common Lisp将要被ANSI标准化,有着好的特性,有很好的环境,并且和其他的语言和软件有着很好的集成.
But, as a business, Lisp is considered to be in ill health. There are persistent and sometimes true rumors about the abandonment of Lisp as a vehicle for delivery of practical applications.
但是从商业化的角度来看,Lisp被视为是不健康的.有一些一直存在的和时不时像真的一样的关于Lisp要放弃作为一种实际应用开发语言的谣言.
To some extent the problem is one of perception — there are simply better Lisp delivery solutions than are generally believed to exist and to a disturbing extent the problem is one of unplaced or misplaced resources, of projects not undertaken, and of implementation strategies not activated.
在某些程度上来说这个问题是一种感性的认识—存在着一种比现在人们通常认为的更好的Lisp的交付解决方案并且有一些令人不安的问题在未放置或正确放置的资源,项目未启动和实现策略未激活.(这一段没能非常理解,还是看原文好)
Part of the problem stems from our very dear friends in the artificial intelligence (AI) business. AI has a number of good approaches to formalizing human knowledge and problem solving behavior. However, AI does not provide a panacea in any area of its applicability. Some early promoters of AI to the commercial world raised expectation levels too high. These expectations had to do with the effectiveness and deliverability of expert-system-based applications.
这个问题的部分产生于我们的一个在AI部门的很好的朋友.AI有着大量的好的实现方法用来形式化人类的知识和解决问题的行为.然而AI并不是一种在任何领域都适用的万能药.一些早期的把AI推向商业世界的推动者将他们的期望升的太高.这些期望与基于专家系统的应用程序的效率和产能有关.(SICP的教授还在上课时黑过当时的AI和专家系统其实没什么用就是骗钱的)
When these expectations were not met, some looked for scapegoats, which frequently were the Lisp companies, particularly when it came to deliverability. Of course, if the AI companies had any notion about what the market would eventually expect from delivered AI software, they never shared it with any Lisp companies I know about. I believe the attitude of the AI companies was that the Lisp companies will do what they need to survive, so why share customer lists and information with them?
当这些期望得不到满足的时候,有些人就开始寻找替罪羊,通常就是提供Lisp的公司,特别是在产能方面.当然,如果AI公司有任何的关于市场最终想从AI软件中获得什么的理念,他们从来不会和任何Lisp公司分享,就我所知道的来说.我相信AI公司之所以以这种态度来对待Lisp公司是因为他们觉得Lisp公司会做让他们自己生存下来所需要的事,所以为什么要和他们分享客户清单和信息呢?
Another part of the problem is the relatively bad press Lisp got, sometimes from very respectable publications. I saw an article in Forbes (October 16, 1989) entitled Where Lisp Slipped by Julie Pitta. However, the article was about Symbolics and its fortunes. The largest criticisms of Symbolics in the article are that Symbolics believed AI would take off and that Symbolics mistakenly pushed its view that proprietary hardware was the way to go for AI. There was nothing about Lisp in the article except the statement that it is a somewhat obscure programming language used extensively in artificial intelligence.
另一部分的问题是关于Lisp有一些不好的新闻,有时候还来自非常令人尊敬的出版物.我看到在Forbes上的一篇文章标题是_Where Lisp Slipped_,作者是Julie Pitta.然而这篇文章是关于Symbolics和它的命运.文中对Symbolics最大的批评是Symbolics相信AI将要起飞(迅猛发展)并且Symbolics错误的认为专有硬件是AI的发展方向.这篇文章中没有任何关于Lisp的内容除了在声明它是一种在人工智能中被广泛使用的模糊逻辑的编程语言.
It seems a pity for the Lisp business to take a bump partly because Julie thought she could make a cute title for her article out of the name Lisp.
But, there are some real successes for Lisp, some problems, and some ways out of those problems.
这看上去很可惜Lisp商业受到一次打击只是因为Julie认为她可以用上Lisp来为她的文章取一个”可爱”的标题.
但是,Lisp有着一些真正的成功,一些问题和解决这些问题的方法.
1 Lisp’s Successes
As I mentioned, Lisp is in better shape today than it ever has been. I want to review some Lisp success stories.
就像我提到的,Lisp在今天有着从未有过的好环境.我想回顾一些Lisp的成功故事.
1.1 Standardization
A major success is that there is a standard Lisp — Common Lisp. Many observers today wish there were a simpler, smaller, cleaner Lisp that could be standardized, but the Lisp that we have today that is ready for standardization is Common Lisp. This isn’t to say that a better Lisp could not be standardized later, and certainly there should be. Furthermore, like any language, Common Lisp should be improved and changed as needs change.
一个主要的成功是今天有一个Lisp的标准 — Common Lisp.很多的观察者今天都希望有一个更简单,更小巧,更干净的Lisp可以被标准化,但是我们现在有的正准备标准化的Lisp是Common Lisp.这不是说一个更好的Lisp以后就不能被标准化,并且它一定会被标准化.此外,就像任何一种语言一样,Common Lisp应该提升和在需要的地方改进自己.
Common Lisp started as a grassroots effort in 1981 after an ARPA-sponsored meeting held at SRI to determine the future of Lisp. At that time there were a number of Lisps in the US being defined and implemented by former MIT folks: Greenblatt (LMI), Moon and Weinreb (Symbolics), Fahlman and Steele (CMU), White (MIT), and Gabriel and Steele (LLNL). The core of the Common Lisp committee came from this group. That core was Fahlman, Gabriel, Moon, Steele, and Weinreb, and Common Lisp was a coalescence of the Lisps these people cared about.
Common Lisp开始基层(自发性)的努力在1981年在SRI举行的ARPA-sponsored会议决定了Lisp的发展之后.从那时候开始在美国有很多的Lisp被定义和实现由前MIT的人:Greenblatt (LMI), Moon 和 Weinreb (Symbolics), Fahlman 和 Steele (CMU), White (MIT), Gabriel 和 Steele (LLNL).Common Lisp委员会的核心也来源于这些人中.主要成员是:Fahlman, Gabriel, Moon, Steele, 和 Weinreb,并且Common Lisp是这些人所关心的Lisp实现的合并.(大概是这个意思,有点拿不准)
There were other Lisps that could have blended into Common Lisp, but they were not so clearly in the MacLisp tradition, and their proponents declined to actively participate in the effort because they predicted success for their own dialects over any common lisp that was defined by the grassroots effort. Among these Lisps were Scheme, Interlisp, Franz Lisp, Portable Standard Lisp, and Lisp370.
还有其他的Lisps可以被融合进Common Lisp,但是它们在MacLisp传统中不是很清晰(?可能是规范问题),并且它们的支持者拒绝积极参与Common Lisp这项工作,因为他们认为自己的Lisp方言超过了任何用Common Lisp规范创造的Lisp语言.这其中的Lisps有:Scheme, Interlisp, Franz Lisp, Portable Standard Lisp, 和 Lisp370.
And outside the US there were major Lisp efforts, including Cambridge Lisp and Le-Lisp. The humble US grassroots effort did not seek membership from outside the US, and one can safely regard that as a mistake. Frankly, it never occurred to the Common Lisp group that this purely American effort would be of interest outside the US, because very few of the group saw a future in AI that would extend the needs for a standard Lisp beyond North America.
在美国以外的有影响的Lisp包括:Cambridge Lisp 和 Le-Lisp.当时美国微弱的底层努力也没有寻求美国以外的Lisps入会,但是这可以看作是一个失误.坦率的说这个基于美国的组织也没有遇见到会引起美国以外的组织的兴趣,因为当时很少有组织能够看到在AI的发展下需要一个超越北美地区的Lisp的标准.
Common Lisp was defined and a book published in 1984 called /Common Lisp: the Language/ (CLtL). And several companies sprang up to put Common Lisp on stock hardware to compete against the Lisp machine companies. Within four years, virtually every major computer company had a Common Lisp that it had either implemented itself or private-labeled from a Common Lisp company.
Common Lisp在1984年被定义并且出版了一本书叫:Common Lisp: the Language.但是只有少数的几家公司跳出来表示会对Common Lisp进行原生的硬件级别的支持来与Lisp商业公司竞争.四年之后,几乎每一个主流的计算机公司都有一个Common Lisp的实现或者是带有私有标签的Common Lisp.
In 1986, X3J13 was formed to produce an ANSI version of Common Lisp. By then it was apparent that there were significant changes required to Common Lisp to clean up ambiguities and omissions, to add a condition system, and to define object-oriented extensions.
在1986年,X3J13为了制造一个ANSI版本的Common Lisp而成立.在这个时候对于Common Lisp来说很显然需要有重大的变化来消除歧义和漏洞,并且增加分支系统和定义面向对象的继承功能.
After several years it became clear that the process of standardization was not simple, even given a mature language with a good definition. The specification of the Common Lisp Object System (CLOS) alone took nearly two years and seven of the most talented members of X3J13.
几年之后事情变得很明显:标准化的进程不是那么简单的,即使是一门定义良好的语言.仅仅是规范化Common Lisp Object System (CLOS)就花费了X3J13成员中最聪明的7个成员2年时间.
It also became apparent that the interest in international Lisp standardization was growing. But there was no heir apparent to Common Lisp. Critics of Common Lisp, especially those outside the US, focused on Common Lisp’s failures as a practical delivery vehicle.
这也表现出大家对国际性的标准化的Lisp的兴趣在增长.但是Common Lisp没有继承者.对于Common Lisp的批评者,特别是美国之外的人,把Common Lisp的失败聚焦在作为一个实用的交付工具上.
In 1988, an international working group for the standardization of Lisp was formed. That group is called WG16. Two things are absolutely clear: The near-term standard Lisp is Common Lisp; a longer-term standard that goes beyond Common Lisp is desirable.
在1988年,一个为了标准化Lisp的国际性组织成立了.这个组织被称作WG16.两件事情被确定了下来:最近的Lisp标准是Common Lisp;一个超越Common Lisp的长期的标准也是被需要的.
In 1988, the IEEE Scheme working group was formed to produce an IEEE and possibly an ANSI standard for Scheme. This group completed its work in 1990, and the relatively small and clean Scheme is a standard.
在1988年,IEEE Scheme工作小组被成立用来为Scheme制作一个IEEE并且最好是一个ANSI标准.这个组织在1990年完成了工作,然后一个相对小的并且简洁的Scheme成为了标准.
Currently, X3J13 is less than a year away from a draft standard for ANSI Common Lisp; WG16 is stalled because of international bickering; Scheme has been standardized by IEEE, but it is of limited commercial interest.
最近,X3J13在草拟了ANSI Common Lisp标准不到一年的时间内WG16因为国际争议而僵住了;Scheme被IEEE标准化但是限制了商业利益.
Common Lisp is in use internationally, and serves at least as a de facto standard until the always contentious Lisp community agrees to work together.
Common Lisp在国际化中被使用,并且在Lisp社区同意一起工作之前作为着事实上的标准.
1.2 Good Performance
Common Lisp performs well. Most current implementations use modern compiler technology, in contrast to older Lisps, which used very primitive compiler techniques, even for the time. In terms of performance, anyone using a Common Lisp today on almost any computer can expect better performance than could be obtained on single-user PDP-10s or on single-user Lisp machines of mid-1980s vintage. Many Common Lisp implementations have multitasking and non-intrusive garbage collection — both regarded as impossible features on stock hardware ten years ago.
Common Lisp的表现很好.最新的实现使用了现代编译器的技术,跟旧的用了原始的编译器技术的Lisps相比在时间上也有很大的差距.在性能方面,在今天任何一个使用Common Lisp的人几乎在任何电脑上都可以获得比单用户的PDP-10s或者1980年代的单用户的Lisp机器更好的性能表现.很多Common Lisp的实现有多线程和非入侵式的GC,这都是在十年之前认为不可能有原生硬件支持的特性.
In fact, Common Lisp performs well on benchmarks compared to C. The following table shows the ratio of Lisp time and code size to C time and code size for three benchmarks.
事实上,Common Lisp在以C语言为基准的测试中也表现很好.下面的表格展示了在三个基准测试中Lisp的执行时间和代码大小以C为基准的比率.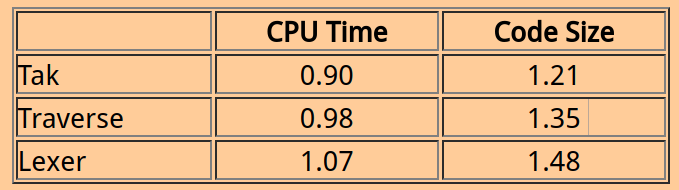
Tak is a Gabriel benchmark that measures function calling and fixnum arithmetic. Traverse is a Gabriel benchmark that measures structure creation and access. Lexer is the tokenizer of a C compiler and measures dispatching and character manipulation.
Tak是一个Gabriel的基准测试主要调用了fixnum算术的函数.Traverse是一个Gabriel基准测试主要是结构体的创造和访问.Lexer是一个是一个C编译器的词法分析器,主要是用来测量调度和元素的操作.
These benchmarks were run on a Sun 3 in 1987 using the standard Sun C compiler using full optimization. The Lisp was not running a non-intrusive garbage collector.
这个基准测试运行在Sun 3 1987年,使用了标准Sun C编译器和全部的优化.Lisp没有运行一个非侵入式的垃圾回收器.
1.3 Good Environments
It is arguable that modern programming environments come from the Lisp and AI tradition. The first bit-mapped terminals (Stanford/MIT), the mouse pointing device (SRI), full-screen text editors (Stanford/MIT), and windowed environments (Xerox PARC) all came from laboratories engaged in AI research. Even today one can argue that the Symbolics programming environment represents the state of the art.
可以说现代的编程环境都是来自于Lisp和传统AI.第一个bit-mapped终端,鼠标点触设备,全屏的文本编辑器,窗口化环境都是来自从事AI研究的实验室.即使是今天,我们也可以认为Symbolics编程环境代表了最先进的技术.
It is also arguable that the following development environment features originated in the Lisp world:
- Incremental compilation and loading
- Symbolic debuggers
- Data inspectors
- Source code level single stepping
- Help on builtin operators
- Window-based debugging
- Symbolic stack backtraces
- Structure editors
可以说下面的开发环境的特性都是源自于Lisp世界的:
- 增量编译和加载
- 符号调试器
- 数据检查
- 原代码级别单步调试
- 内置的帮助操作
- 基于窗口的调试
- 符号栈回溯
- 结构编辑器
Today’s Lisp environments are equal to the very best Lisp machine environments in the 1970s. Windowing, fancy editing, and good debugging are all commonplace. In some Lisp systems, significant attention has been paid to the software lifecycle through the use of source control facilities, automatic cross-referencing, and automatic testing.
今天的Lisp环境和1970年代最好的Lisp机器环境相同.窗口化,联想编辑和良好的Debug都很平常.在一些Lisp系统中,把更多的注意力放在通过软件源来进行软件生命周期
的控制,自动交叉引用和自动测试.
1.4 Good Integration
Today Lisp code can coexist with C, Pascal, Fortran, etc. These languages can be invoked from Lisp and in general, these languages can then re-invoke Lisp. Such interfaces allow the programmer to pass Lisp data to foreign code, to pass foreign data to Lisp code, to manipulate foreign data from Lisp code, to manipulate Lisp data from foreign code, to dynamically load foreign programs, and to freely mix foreign and Lisp functions.
今天,Lisp代码可以和C,Pascal,Fortran等等代码共存.这些语言可以从Lisp被调用,并且一般的这些语言也可以重新调用Lisp.这样的接口允许程序员传递Lisp数据给其他的代码,或者把其他代码的数据传进来,从Lisp代码操作外部数据,从外部代码来操作Lisp数据,动态加载外部程序并且可以自由的混合外部和Lisp函数.
The facilities for this functionality are quite extensive and provide a means for mixing several different languages at once.
这种功能被广泛的应用并且可以一次性混合几种不同的语言.
1.5 Object-oriented Programming
Lisp has the most powerful, comprehensive, and pervasively object-oriented extensions of any language. CLOS embodies features not found in any other object-oriented language. These include the following:
- Multiple inheritance
- Generic functions including multi-methods
- First-class classes
- First-class generic functions
- Metaclasses
- Method combination
- Initialization protocols
- Metaobject protocol
- Integration with Lisp types
Lisp有着最强大,最全面和最广泛的面向对象拓展相对任何语言.CLOS体现了其他任何一门面向对象语言都没有的特性.包括一下几点:
- 多重继承
- 生成包括多个方法的函数
- classes作为一等公民
- 生成函数作为一等公民
- 元类
- 方法的组合
- 初始化协议
- 元类协议
- 与Lisp类的集成
It is likely that Common Lisp (with CLOS) will be the first standardized object-oriented programming language.
看上去似乎Common Lisp将要成为第一个被标准化的面向对象的编程语言
1.6 Delivery
It is possible to deliver applications written in Lisp. The currently available tools are good but are not yet ideal. These solutions include from removing unused code and data from application, building up applications using only the code and data needed, and producing .o files from Lisp code.
Delivery tools are commercially provided by Lucid, Franz, and Ibuki.
用Lisp来编写可以交付的应用是可能的.现在可用的工具挺好但是还不是最理想的.这个解决方案包括从应用中移除未使用的代码和数据,只使用需要的代码和数据来构建应用和从Lisp代码生产出.o文件
交付工具商业提供由Lucid, Franz, 和 Ibuki提供.
2 Lisp’s Apparent Failures
Too many teardrops for one heart to be crying.
Too many teardrops for one heart to carry on.
You’re way on top now, since you left me,
Always laughing, way down at me.
— The Mysterians
This happy story, though, has a sad interlude, an interlude that might be attributed to the failure of AI to soar, but which probably has some other grains of truth that we must heed. The key problem with Lisp today stems from the tension between two opposing software philosophies. The two philosophies are called The Right Thing and Worse is Better.
这个快乐的故事却有一个悲伤的插曲,一个可能归因于AI没有腾飞的插曲,但是可能还有一些其他的事实需要我们注意.Lisp今天的主要问题源于两种软件开发哲学之间的关系.这2种哲学称为做正确的事和差一点的更好.
2.1 The Rise of Worse is Better
I and just about every designer of Common Lisp and CLOS has had extreme exposure to the MIT/Stanford style of design. The essence of this style can be captured by the phrase the right thing. To such a designer it is important to get all of the following characteristics right:
- Simplicity — the design must be simple, both in implementation and interface. It is more important for the interface to be simple than the implementation.
- Correctness — the design must be correct in all observable aspects. Incorrectness is simply not allowed.
- Consistency — the design must not be inconsistent. A design is allowed to be slightly less simple and less complete to avoid inconsistency. Consistency is as important as correctness.
- Completeness — the design must cover as many important situations as is practical. All reasonably expected cases must be covered. Simplicity is not allowed to overly reduce completeness.
我和几乎所有的Common Lisp和CLOS的设计者都深受MIT/Stanford风格的影响.这种风格可以用_the right thing_这个短语来概括.对于这样的设计者来说重要的是要复合下面的所有特征:
简洁 — 设计必须是简洁的,在实现和接口上都需要保证简洁.接口的简洁性要比代码实现的简洁更重要
正确 — 在可以观察到的所有方面都必须保证正确性.不正确的事是不允许的.
一致 — 设计不能不一致.一个保持一致性的设计可以允许丢失一些简洁性而避免不一致.一致性比正确性更加重要.
完整 — 设计必须涵盖尽可能多的重要的应用情形.所有能预期的合理的情形都必须被包含.不能为了保证简洁性而降低系统的完整度.
I believe most people would agree that these are good characteristics. I will call the use of this philosophy of design the MIT approach Common Lisp (with CLOS) and Scheme represent the MIT approach to design and implementation.
我相信大部分的人都会认为这是一种好的程序开发方式.我把使用这种软件设计理念称为MIT方法,Common Lisp和Scheme是MIT方法设计和实现软件的代表.
The worse-is-better philosophy is only slightly different:
- Simplicity — the design must be simple, both in implementation and interface. It is more important for the implementation to be simple than the interface. Simplicity is the most important consideration in a design.
- Correctness — the design must be correct in all observable aspects. It is slightly better to be simple than correct.
- Consistency — the design must not be overly inconsistent. Consistency can be sacrificed for simplicity in some cases, but it is better to drop those parts of the design that deal with less common circumstances than to introduce either implementational complexity or inconsistency.
- Completeness — the design must cover as many important situations as is practical. All reasonably expected cases should be covered. Completeness can be sacrificed in favor of any other quality. In fact, completeness must be sacrificed whenever implementation simplicity is jeopardized. Consistency can be sacrificed to achieve completeness if simplicity is retained; especially worthless is consistency of interface.
差一点更好的设计理念只有一些细微的差别:
简洁 — 设计必须是简洁的,在实现和接口上都需要保证简洁.接口的简洁性要比代码实现的简洁更重要.简洁性是软件设计中最值得重视的方面.
正确 — 在可以观察到的所有方面都必须保证正确性.在设计中多一点简洁性比正确性更好
一致 — 设计不能过于矛盾.在某些情况下一致性可以为简洁性让步,但是比起为了处理少数不常见的情况增加实现的复杂度和不一致性来,丢掉他们反而更好.
完整 — 设计必须涵盖到常见的重要情形.所有合理的预期情况都应该被包含.但是为了其他几种特质,可以牺牲完整性.事实上,当危及到实现的简洁性时完整性可以被牺牲.为了实现的完整性可以牺牲一致性;接口的一致性是最没用的.
Early Unix and C are examples of the use of this school of design, and I will call the use of this design strategy the New Jersey approach I have intentionally caricatured the worse-is-better philosophy to convince you that it is obviously a bad philosophy and that the New Jersey approach is a bad approach.
早期Unix和C就是使用这种设计理念的代表,我将这种设计方式称之为New Jersey(新泽西)设计方法并且我有意讽刺这种差一点更好的理念并且试图说服人们这显然是一种不好的软件设计哲学,新泽西理念是一种不好的理念.
However, I believe that worse-is-better, even in its strawman form, has better survival characteristics than the-right-thing, and that the New Jersey approach when used for software is a better approach than the MIT approach.
然而,我相信这种差一点更好的设计理念在假象情况会比正确的做法有更强的生存力,在软件开发上新泽西方法要比MIT方法更好.
Let me start out by retelling a story that shows that the MIT/New-Jersey distinction is valid and that proponents of each philosophy actually believe their philosophy is better.
让我来复述一个故事用来展示MIT方法和New-Jersey方法之间的区别,以及为什么每一种理念的支持者都坚信他们的理念更好.
Two famous people, one from MIT and another from Berkeley (but working on Unix) once met to discuss operating system issues. The person from MIT was knowledgeable about ITS (the MIT AI Lab operating system) and had been reading the Unix sources. He was interested in how Unix solved the PC loser-ing problem. The PC loser-ing problem occurs when a user program invokes a system routine to perform a lengthy operation that might have significant state, such as IO buffers. If an interrupt occurs during the operation, the state of the user program must be saved. Because the invocation of the system routine is usually a single instruction, the PC of the user program does not adequately capture the state of the process. The system routine must either back out or press forward. The right thing is to back out and restore the user program PC to the instruction that invoked the system routine so that resumption of the user program after the interrupt, for example, re-enters the system routine. It is called PC loser-ing because the PC is being coerced into loser mode, where loser is the affectionate name for user at MIT.
两个著名人物,一个来自MIT另一个来自伯利克里,一次他们遇到并且讨论操作系统的问题.来自MIT的人对ITS很熟悉并且他阅读过Unix的源码.他对Unix如何解决PC的loser-ing问题很感兴趣.当一个用户调用了一个系统程序去执行一个长时间的操作的时候就有可能出现loser-ing问题,例如I/O缓冲.如果在这个操作的时候发生了一个中断,那么用户程序的状态就必须要被保存.因为系统程序的调用通常都是单指令的,运行用户程序的PC不能捕获这个系统程序的状态.系统程序这时候只能被退出或者继续执行.正确的做法是退出并且重新装载用户程序调用系统程序的指令,这样可以让用户程序在中断之后继续执行,例如,重新进入系统程序.因为这时候PC被迫进入了一种弱势的状态所以这个问题被称为PC loser-ing问题,loser是MIT对用户的一种”爱称”.
The MIT guy did not see any code that handled this case and asked the New Jersey guy how the problem was handled. The New Jersey guy said that the Unix folks were aware of the problem, but the solution was for the system routine to always finish, but sometimes an error code would be returned that signaled that the system routine had failed to complete its action. A correct user program, then, had to check the error code to determine whether to simply try the system routine again. The MIT guy did not like this solution because it was not the right thing.
MIT的人没有看到处理这种情况的代码然后问新泽西的人是怎么解决这个问题的.新泽西的人说Unix的人也意识到了这个问题,但是因为这个问题中系统进程通常是可以结束的,所以在问题出现的时候会返回一个错误码来表示没能执行完这个系统进程.一个正确的用户进程这时候需要去检查错误码来决定要不要再执行这个系统进程.MIT的人不喜欢这种解决方法因为这不是在做正确的事.
The New Jersey guy said that the Unix solution was right because the design philosophy of Unix was simplicity and that the right thing was too complex. Besides, programmers could easily insert this extra test and loop. The MIT guy pointed out that the implementation was simple but the interface to the functionality was complex. The New Jersey guy said that the right tradeoff has been selected in Unix — namely, implementation simplicity was more important than interface simplicity.
新泽西的人说Unix的这种解决办法是正确的因为Unix的设计哲学是保持简洁而且在这个问题上正确的做法太麻烦.除此之外,程序员可以很容易的插入对(返回错误码)的测试和(重启)的循环.MIT的人指出这样的实现是很简洁但是接口的功能性太复杂了.新泽西人说这是Unix做的正确的权衡 — 也就是说,实现上的简洁性比接口的简洁性更加重要.
The MIT guy then muttered that sometimes it takes a tough man to make a tender chicken, but the New Jersey guy didn’t understand (I’m not sure I do either).
MIT的人抱怨到:那有时候你就要让一个强壮的人变成一只弱小的鸡,但是新泽西人没有能够明白(我也没能明白).
Now I want to argue that worse-is-better is better. C is a programming language designed for writing Unix, and it was designed using the New Jersey approach. C is therefore a language for which it is easy to write a decent compiler, and it requires the programmer to write text that is easy for the compiler to interpret. Some have called C a fancy assembly language. Both early Unix and C compilers had simple structures, are easy to port, require few machine resources to run, and provide about 50%-80% of what you want from an operating system and programming language.
现在我想说差一点更好的设计方式更好.C语言被设计用来写Unix并且是用新泽西方式实现的.也因此C可以简单的写出一个比较正经的编译器,并且它要求程序员写的代码要方便给编译器解释.也有人因此称C是一种花哨的汇编语言.早起的Unix和C语言都有简单的结构,易于移植,只需要很少的资源就可以运行并且能够提供你所需要的50%-80%的操作系统和编程语言的功能.
Half the computers that exist at any point are worse than median (smaller or slower). Unix and C work fine on them. The worse-is-better philosophy means that implementation simplicity has highest priority, which means Unix and C are easy to port on such machines. Therefore, one expects that if the 50% functionality Unix and C support is satisfactory, they will start to appear everywhere. And they have, haven’t they?
现在的电脑有一半在任何方面都比中等(性能)还要差(更小或者更慢).Unix和C都在上面运行的很好.差一点更好的设计理念意味着实现的简洁性有最高的优先级,这也就意味着Unix和C很容易移植到任何机器上.因此,如果说Unix和C能实现50%的期待,那么就会出现在任何地方.并且它们做到了,不是吗?
Unix and C are the ultimate computer viruses.
Unix和C是终极电脑病毒.
A further benefit of the worse-is-better philosophy is that the programmer is conditioned to sacrifice some safety, convenience, and hassle to get good performance and modest resource use. Programs written using the New Jersey approach will work well both in small machines and large ones, and the code will be portable because it is written on top of a virus.
差一点更好的设计理念的一个更长远的好处是:程序员可以考虑牺牲一部分的安全性和便利性来争取获得更好的性能和更少的资源使用.使用新泽西实现的程序员将会在小型机器和大型机器上都能工作的很好,并且代码会有很高的可移植性因为它们是用最好的病毒写出来的.
It is important to remember that the initial virus has to be basically good. If so, the viral spread is assured as long as it is portable. Once the virus has spread, there will be pressure to improve it, possibly by increasing its functionality closer to 90%, but users have already been conditioned to accept worse than the right thing. Therefore, the worse-is-better software first will gain acceptance, second will condition its users to expect less, and third will be improved to a point that is almost the right thing. In concrete terms, even though Lisp compilers in 1987 were about as good as C compilers, there are many more compiler experts who want to make C compilers better than want to make Lisp compilers better.
需要牢记的很重要的一点是:初始病毒要足够的好.这样的话,只要病毒是可移植的就能保证它的传播.一旦病毒传播开来,就会有改进的压力,大概会让它的功能增加到90%左右,但是这时候用户早已经习惯了接受那些不足的地方相比于做正确的软件来说.因此,差一点更好的软件首先将会获得接受,然后会降低用户的期望,然后改进这些点直到完全接近正确的软件.在实际情况中,尽管在1987年Lisp编译器比C编译器更好,但是更多的编译器专家试图让C编译器变得更好相比于Lisp编译器来说.
The good news is that in 1995 we will have a good operating system and programming language; the bad news is that they will be Unix and C++.
好消息是在1995年我们就有了一个好的操作系统和编程语言,坏消息是他们变成了Unix和C++.
There is a final benefit to worse-is-better. Because a New Jersey language and system are not really powerful enough to build complex monolithic software, large systems must be designed to reuse components. Therefore, a tradition of integration springs up.
差一点更好的设计理念还有最后一个好处.因为新泽西语言和系统没有足够的能力来构建一个复杂的独立系统,一个大型的系统一定要被设计成可重用的组件.因此,一种整合的传统就此涌现了.
How does the right thing stack up? There are two basic scenarios: the big complex system scenario and the diamond-like jewel scenario.
正确的做法应该是怎么样的呢?有两种基本方案:复杂的大型系统方案和钻石般宝石方案.
The big complex system scenario goes like this:
复杂的大型系统方案看上去是这样的:
First, the right thing needs to be designed. Then its implementation needs to be designed. Finally it is implemented. Because it is the right thing, it has nearly 100% of desired functionality, and implementation simplicity was never a concern so it takes a long time to implement. It is large and complex. It requires complex tools to use properly. The last 20% takes 80% of the effort, and so the right thing takes a long time to get out, and it only runs satisfactorily on the most sophisticated hardware.
首先,需要好好设计如何做正确的事.它的实现也需要被设计.最后系统被实现出来了.因为这是在做正确的事,需要几乎100%的预期功能,因为实现的简洁性不需要被考虑所以需要花很长的时间去实现它.这是一个很大和很复杂的工程,需要正确使用复杂的工具.最后20%的功能会花去80%的精力,所以做正确的事需要花很长的时间,并且它只有在最尖端的设备上才能很好的运行.
The diamond-like jewel scenario goes like this:
钻石般珠宝的方案看上去是这样的:
The right thing takes forever to design, but it is quite small at every point along the way. To implement it to run fast is either impossible or beyond the capabilities of most implementors.
做正确的事的做法花了大量的时间去设计,但是每个功能点却十分的小.想要让这种实现运行的的很快是不可能的或者说是超出了大部分的开发者的能力的.
The two scenarios correspond to Common Lisp and Scheme.
第二种场景对应的是Common Lisp和Scheme.
The first scenario is also the scenario for classic artificial intelligence software.
第一种场景也通常是经典的人工智能软件的开发场景.
The right thing is frequently a monolithic piece of software, but for no reason other than that the right thing is often designed monolithically. That is, this characteristic is a happenstance.
做正确的事做出来的往往是一个单一的软件,但是没有理由除了做正确的事这种方法之外的方法也会做出单一的软件来,所以这个特征是偶然的.
The lesson to be learned from this is that it is often undesirable to go for the right thing first. It is better to get half of the right thing available so that it spreads like a virus. Once people are hooked on it, take the time to improve it to 90% of the right thing.
从这件事中我们学到的是,一开始就来做正确的事是不可取的.更好的做法是先完成正确的事的一半,可以使得传播的速度像病毒一样.一旦人们迷上了它,再花时间做到正确的事的90%.
A wrong lesson is to take the parable literally and to conclude that C is the right vehicle for AI software. The 50% solution has to be basically right, and in this case it isn’t.
一个错误的认识是只看了表面意思觉得C语言是做AI软件的正确的轮子.在只做50%正确的事的解决上基本是没问题的,但是在AI软件上不行.
But, one can conclude only that the Lisp community needs to seriously rethink its position on Lisp design. I will say more about this later.
但是,有一点我们可以下结论的是:Lisp社区需要认真思考一下Lisp的设计.在下面我会讨论更多.
2.2 Good Lisp Programming is Hard
Many Lisp enthusiasts believe that Lisp programming is easy. This is true up to a point. When real applications need to be delivered, the code needs to perform well. With C, programming is always difficult because the compiler requires so much description and there are so few data types. In Lisp it is very easy to write programs that perform very poorly; in C it is almost impossible to do that. The following examples of badly performing Lisp programs were all written by competent Lisp programmers while writing real applications that were intended for deployment. I find these quite sad.
很多的Lisp爱好者都相信Lisp编程是很简单的.在某种程度上是正确的.当一个真实的应用需要被交付的时候,代码需要表现的很好.用C语言编程总是很困难的因为编译器需要很多的描述并且它只有少数的几种数据类型.在Lisp中,编写性能非常差的代码是很简单的,但是在C语言里这几乎是不可能的.下面的例子里表现的很差的Lisp程序都是由有能力的Lisp程序员在开发实际应用的时候写的.我对此很难过.
2.2.1 Bad Declarations 糟糕的声明方式
This example is a mistake that is easy to make. The programmer here did not declare his arrays as fully as he could have. Therefore, each array access was about as slow as a function call when it should have been a few instructions. The original declaration was as follows:
(proclaim '(type (array fixnum *) *ar1* *ar2* *ar3*))
这个例子是一个很容易犯的错误,程序员没有能够很清楚的声明数组.因此对每一个数组的访问都像函数调用一样慢.原本的声明如下:(proclaim '(type (array fixnum *) *ar1* *ar2* *ar3*))
The three arrays happen to be of fixed size, which is reflected in the following correct declaration:
在这三个数组被填充的时候,应该写成下面这种正确的方式:
1 | (proclaim '(type (simple-array fixnum (4)) *ar1*)) |
Altering the faulty declaration improved the performance of the entire system by 20%.
修改这些不完善的声明可以提高整个系统20%的性能.
2.2.2 Poor Knowledge of the Implementation
The next example is where the implementation has not optimized a particular case of a general facility, and the programmer has used the general facility thinking it will be fast. Here five values are being returned in a situation where the order of side effects is critical:
下一个例子是一个没有对一个常见的情况进行优化,因为程序员习惯于这种通常的代码形式而且觉得它会很快.代码中的五个值将会在顺序的副作用的影响下被返回.
1 | (multiple-value-prog1 |
The implementation happens to optimize multiple-value-prog1 for up to three return values, but the case of five values CONSes. The correct code follows:
正确的实现是优化multiple-value-prog1只返回至多三个值,返回五个值的情况太复杂了.正确的代码如下:
1 | (let ((x1 (f1 x)) |
There is no reason that a programmer should know that this rewrite is needed. On the other hand, finding that performance was not as expected should not have led the manager of the programmer in question to conclude, as he did, that Lisp was the wrong language.
程序员没有理由需要知道怎么重写.从另一方面来说,程序的性能不如预期的表现的好也不能使得程序员的管理者得出Lisp是一门错误语言的结论.
2.2.3 Use of FORTRAN Idioms
Some Common Lisp compilers do not optimize the same way as others. The following expression is sometimes used:
有些Common Lisp的编译器不像其他的一样优化.下面的表达式有时候被使用:
(* -1 <form>)
when compilers often produce better code for this variant:
一般情况下编译器会生成出更好的代码:
(- <form>)
Of course, the first is the Lisp analog of the FORTRAN idiom:
当然,第一个代码是FORTRAN的习惯用法在Lisp里使用(不是很懂):
`- -1*<form>`2.2.4 Totally Inappropriate Data Structures
Some might find this example hard to believe. This really occurred in some code I’ve seen:
有人会觉得下面的例子难以置信.但是这真的出现在我看过的代码里:
1 | (defun make-matrix (n m) |
What’s worse is that in the particular application, the matrices were all fixed size, and matrix arithmetic would have been just as fast in Lisp as in FORTRAN.
这个代码的问题在于在特定的应用下,矩阵的大小是固定的,并且矩阵的运算效率在Lisp中会和FORTRAN一样快.
This example is bitterly sad: The code is absolutely beautiful, but it adds matrices slowly. Therefore it is excellent prototype code and lousy production code. You know, you cannot write production code as bad as this in C.
这个例子让人难过的是:代码看上去确实很漂亮,但是对矩阵求和太慢了.因此这是很优秀的原型代码但是是很差的生产代码.你知道你在C语言中不可能写出这么差的生产代码.
2.3 Integration is God
In the worse-is-better world, integration is linking your .o files together, freely intercalling functions, and using the same basic data representations. You don’t have a foreign loader, you don’t coerce types across function-call boundaries, you don’t make one language dominant, and you don’t make the woes of your implementation technology impact the entire system.
在差一点更好的世界里,集成就是把你的.o文件都链接在一起,自由的衔接功能,并且使用相同的基本的数据表示.你不必做额外的装载操作,你不必做强制的类型要求在进行跨界的函数调用的时候,你不需要使用一种语言来主导,并且你不会让技术上的实现的困难影响到整个系统.
The very best Lisp foreign functionality is simply a joke when faced with the above reality. Every item on the list can be addressed in a Lisp implementation. This is just not the way Lisp implementations have been done in the right thing world.
在面对上面的问题的时候最好的Lisp的外部调用会让它简单的像一个笑话.列出的每一项都可以在Lisp中被实现.只是这不是Lisp在做正确事的世界中的实现方式而已.
The virus lives while the complex organism is stillborn. Lisp must adapt, not the other way around. The right thing and 2 shillings will get you a cup of tea.
当复杂的有机体死亡的时候,病毒可以活下去.Lisp必须适应而不是相反.做正确的事和2先令将会给你一杯茶(??理解不能,可能是用Lisp会变得很轻松)
2.4 Non-Lisp Environments are Catching Up
This is hard to face up to. For example, most C environments — initially imitative of Lisp environments — are now pretty good. Current best C environments have the following:
- Symbolic debuggers
- Data inspectors
- Source code level single stepping
- Help on builtin operators
- Window-based debugging
- Symbolic stack backtraces
- Structure editors
这是很难面对的一件事.例如:大部分的C的环境 — 是模仿Lisp环境的 — 现在变得相当好. 现在最好的C的环境是下面这样的:
符号调试工具
数据检查
源代码级别的单步调试
内置的帮助操作
基于窗口的调试
符号化的调用栈的回溯
结构编辑
And soon they will have incremental compilation and loading. These environments are easily extendible to other languages, with multi-lingual environments not far behind.
并且很快的他们将会有渐进编译和加载.这些环境很容易拓展到其他的语言,并且多语言的环境也不远了.
Though still the best, current Lisp environments have several prominent failures. First, they tend to be window-based but not well integrated. That is, related information is not represented so as to convey the relationship. A multitude of windows does not mean integration, and neither does being implemented in the same language and running in the same image. In fact, I believe no currently available Lisp environment has any serious amount of integration.
虽然现在Lisp还是最好的,但是还是有几个突出的错误.第一,它们是基于窗口的,但是集成的不够好.就是说,相关的信息没有被表示成关系的形式.多个窗口并不意味着就是集成,并且也没有实现相同的语言和运行在同一个情景中.事实上,我相信没有一个现成的Lisp环境有任何这样的集成.
Second, they are not persistent. They seemed to be defined for a single login session. Files are used to keep persistent data — how 1960s.
第二,他们并不执着.似乎(Lisp环境)就是给单个的登录会话使用的.文件被用来保存持久化数据 — 就像在1960年代一样
Third, they are not multi-lingual even when foreign interfaces are available.
第三,他们没有多语言甚至外部接口已经可用了.
Fourth, they do not address the software lifecycle in any extensive way. Documentation, specifications, maintenance, testing, validation, modification, and customer support are all ignored.
第四,他们没有用广泛的方式解决软件生命周期的问题.文档,规范,维护,测试,验证,修改和用户支持都被忽视了.
Fifth, information is not brought to bear at the right times. The compiler is able to provide some information, but the environment should be able to generally know what is fully defined and what is partially defined. Performance monitoring should not be a chore.
第五,不能在适当的时候提供一些信息.编译器是可以提供一些信息,但是环境应该知道什么是完全定义的什么是部分定义的.性能监控不是一件苦差事.
Sixth, using the environment is difficult. There are too many things to know. It’s just too hard to manage the mechanics.
第六,使用Lisp的环境太困难了.需要知道很多的东西.而且管理机器太困难了.
Seventh, environments are not multi-user when almost all interesting software is now written in groups.
第七,环境里没有多用户的支持然而现在几乎所有有趣的软件都是由小组编写的.
The real problem has been that almost no progress in Lisp environments has been made in the last 10 years.
而真正的问题是在最近10年Lisp环境几乎没有取得进展.
3 How Lisp Can Win Big
1 | When the sun comes up, I’ll be on top. |
The gloomy interlude can have a happy ending.
在阴沉的插曲之后可以有一个好的结局.
3.1 Continue Standardization Progress
We need to bury our differences at the ISO level and realize that there is a short term need, which must be Common Lisp, and a long term need, which must address all the issues for practical applications.
我们需要在ISO层面上埋葬差异并且在短期内实现,例如是Common Lisp,并且有一个长期的需求来解决所有的实际应用的问题.
We’ve seen that the right thing attitude has brought us a very large, complex-to-understand, and complex-to-implement Lisp — Common Lisp that solves way too many problems. We need to move beyond Common Lisp for the future, but that does not imply giving up on Common Lisp now. We’ve seen it is possible to do delivery of applications, and I think it is possible to provide tools that make it easier to write applications for deployment. A lot of work has gone into getting Common Lisp to the point of a right thing in many ways, and there are viable commercial implementations. But we need to solve the delivery and integration problems in spades.
我们已经看到了做正确的事的意见给我们带来了一个非常巨大,很难理解并且实现起来很复杂的Lisp —Common Lisp解决了这其中的很多问题.我们需要在未来超过Common Lisp,但是这不意味着现在就要放弃Lisp.我们已经看到用Lisp来提供应用是可能的,我认为提供便于开发的工具也是可能的.在让Common Lisp做正确的事的路上已经做了很多的工作,并且有商业实现.但是我们还是需要解决交付和集成上的问题.
Earlier I characterized the MIT approach as often yielding stillborn results. To stop Common Lisp standardization now is equivalent to abortion, and that is equivalent to the Lisp community giving up on Lisp. If we want to adopt the New Jersey approach, it is wrong to give up on Lisp, because C just isn’t the right language for AI.
早些时候我觉得MIT的实现方法就是经常导致项目流产的结果.现在停止Common Lisp的标准化就等于是让它堕胎,也说明Lisp的社区放弃了Lisp.如果我们想要采取新泽西的实现方法,放弃Lisp就是错误的,因为C语言对AI来说也不是一门正确的语言.
It also simply is not possible to dump Common Lisp now, work on a new standard, and then standardize in a timely fashion. Common Lisp is all we have at the moment. No other dialect is ready for standardization.
现在也无法直接抛弃Common Lisp然后在一个新的标准下工作,然后及时标准化.Common Lisp是我们现在的全部了.没有别的一门方言已经准备好标准化了.
Scheme is a smaller Lisp, but it also suffers from the MIT approach. It is too tight and not appropriate for large-scale software. At least Common Lisp has some facilities for that.
Scheme是一门更小的Lisp,但是它也在遭受MIT实现之苦.它太过于轻量级并且没有大规模的软件.最起码Common Lisp现在还有一些设备在运行.
I think there should be an internationally recognized standard for Common Lisp. I don’t see what is to be gained by aborting the Common Lisp effort today just because it happens to not be the best solution to a commercial problem. For those who believe Lisp is dead or dying, what does killing off Common Lisp achieve but to convince people that the Lisp community kills its own kind? I wish less effort would go into preventing Common Lisp from becoming a standard when it cannot hurt to have several Lisp standards.
我认为Common Lisp应该有一个国际认可的标准.我不能理解今天努力让Common Lisp流产的目的是什么,难道仅仅只是因为它不是商业问题最好的解决方案?对于那些相信Lisp已死或者正在死亡的人,杀死了Common Lisp的实现还要使人们相信是Lisp社区杀死了Lisp?我希望这些人对于Common Lisp的标准化有更少的影响当它不会伤害到Lisp并且只有少数几个标准的时候.
On the other hand, there should be a strong effort towards the next generation of Lisp. The worst thing we can do is to stand still as a community, and that is what is happening.
换句话说,他们应该对下一代的Lisp有更多的影响.我们现在能做的最差的事就是作为一个社区而原地不动,并且这正在发生.
All interested parties must step forward for the longer-term effort.
所有有关方面都必须向前迈进,以实现长期的影响.
3.2 Retain the High Ground in Environments
I think there is a mistake in following an environment path that creates monolithic environments. It should be possible to use a variety of tools in an environment, and it should be possible for those who create new tools to be able to integrate them into the environment.
我认为创建一个单一环境的路径是有问题的.应该可以在环境中使用各种工具,而且当有人创造了新的工具的时候可以被集成进去.
I believe that it is possible to build a tightly integrated environment that is built on an open architecture in which all tools, including language processors, are protocol-driven. I believe it is possible to create an environment that is multi-lingual and addresses the software lifecycle problem without imposing a particular software methodology on its users.
我相信在一个有所有工具的开放的架构上构建一个紧密集成的环境是有可能的,包括语言的处理和协议驱动.我相信有可能创建一个有多种语言的环境并且解决软件生命周期的问题在不用给用户强加特定的软件方法之下.
Our environments should not discriminate against non-Lisp programmers the way existing environments do. Lisp is not the center of the world.
我们的环境不应该像现在这样区别对待非Lisp程序员.Lisp不是世界的中心.
3.3 Implement Correctly
Even though Common Lisp is not structured as a kernel plus libraries, it can be implemented that way. The kernel and library routines can be in the form of .o files for easy linking with other, possibly non-Lisp, modules; the implementation must make it possible to write, for example, small utility programs. It is also possible to piggyback on existing compilers, especially those that use common back ends. It is also possible to implement Lisp so that standard debuggers, possibly with extensions, can be made to work on Lisp code.
虽然Common Lisp不是内核附加库的一部分,但是它可以被这样实现.内核和lib库程序可以很轻松的链接东西的文件以.o文件的形式,可能是非Lisp,模块;这种实现必须能够编写,例如,小的工具程序.它也必须被附带在现有的编译器中,特别是公用后端的人.也可以用来实现Lisp以便可以使用标准调试器,可能带有拓展,可以处理Lisp代码.
It might take time for developers of standard tools to agree to extend their tools to Lisp, but it certainly won’t happen until our (exceptional) language is implemented more like ordinary ones.
标准工具的开发人员可能会花一点时间才会拓展他们的工具到Lisp,但是这在我们实现更普通的语言之前是不会发生的.
3.4 Achieve Total Integration
I believe it is possible to implement a Lisp and surrounding environment which has no discrimination for or against any other language. It is possible using multi-lingual environments, clever representations of Lisp data, conservative garbage collection, and conventional calling protocols to make a completely integrated Lisp that has no demerits.
我相信在不歧视其他任何语言的同时实现Lisp和周边生态环境是可能的.可能使用多语言环境,Lisp数据的巧妙表示,保守的垃圾收集和传统的调用协议,使得集成的Lisp没有任何缺点.
3.5 Make Lisp the Premier Prototyping Language
Lisp is still the best prototyping language. We need to push this forward. A multi-lingual environment could form the basis or infrastructure for a multi-lingual prototyping system. This means doing more research to find new ways to exploit Lisp’s strengths and to introduce new ones.
Lisp仍旧是最好的元语言.我们需要继续推行.一个多语言的环境可以从基础或者多语言原系统而来.这意味着需要更多的研究来找到新的发挥Lisp的优势并引入的方法.
Prototyping is the act of producing an initial implementation of a complex system. A prototype can be easily instrumented, monitored, and altered. Prototypes are often built from disparate parts that have been adapted to a new purpose. Descriptions of the construction of a prototype often involve statements about modifying the behavioral characteristics of an existing program. For example, suppose there exists a tree traversal program. The description of a prototype using this program might start out by saying something like
元编程是产生一个复杂系统的初始行为.元类型可以很容易进行检测,监控和修改.元类型通常是根据已经适应了新的目标的部分构建的.对元类型构造的描述通常涉及关于修改现有程序的行为特征的陈述.例如,存在一个树遍历程序.使用这个程序的元类型的描述可能从说出像:
S1 be the sequence of leaf nodes visited by P on tree T1 and S2 the
1 | leaf nodes visited by P on tree T2. Let C be a correspondence between |
Subsequent statements might manipulate the correspondence and use f. Once the definition of a leaf node is made explicit, this is a precise enough statement for a system to be able to modify the traversal routine to support the correspondence and f.
后续语句可能会操纵对应关系并使用f.一旦叶节点的定义明确,这对系统来说就是一个足够精确的语句能够修改遍历例程以支持对应关系和f.
A language that describes the modification and control of an existing program can be termed a program language. Program languages be built on one or several underlying programming languages, and in fact can be implemented as part of the functionality of the prototyping environment. This view is built on the insight that an environment is a mechanism to assist a programmer in creating a working program, including preparing the source text. There is no necessary requirement that an environment be limited to working only with raw source text. As another example, some systems comprise several processes communicating through channels. The creation of this part of the system can be visual, with the final result produced by the environment being a set of source code in several languages, build scripts, link directives, and operating system calls. Because no single programming language encompasses the program language, one could call such a language an epi-language.
一种语言可以描述修改和控制的语言可以称为程序语言.程序语言可以基于一种或多种底层编程语言构建,事实上,它可以作为原型设计环境功能的一部分来实现.这种观点是建立于这种看法之上的:环境是用来帮助程序员创建一个运行的程序的,包括准备源文件.没有必要要求一个环境被限制为只能工作在源文件中.作为另一个例子,一些系统包括通过信道通信的若干进程.这部分系统的创建可以是可视化的,环境产生的最终结果是一组多种语言的源代码,构建脚本,链接指令和操作系统调用.因为没有一种编程语言包含程序语言,所以可以将这种语言称为epi语言.
3.6 The Next Lisp
I think there will be a next Lisp. This Lisp must be carefully designed, using the principles for success we saw in worse-is-better.
我认为会有下一代的Lisp.这个Lisp一定会被很好的设计,使用在差一点更好中成功的准则.
There should be a simple, easily implementable kernel to the Lisp. That kernel should be both more than Scheme — modules and macros — and less than Scheme — continuations remain an ugly stain on the otherwise clean manuscript of Scheme.
应该有一个简洁的,易于实现的Lisp的内核.这个内核在宏和模块上要强于Scheme并且比Scheme更小.延续(Scheme)是一个污点换句话说要清理Scheme的污点.
The kernel should emphasize implementational simplicity, but not at the expense of interface simplicity. Where one conflicts with the other, the capability should be left out of the kernel. One reason is so that the kernel can serve as an extension language for other systems, much as GNU Emacs uses a version of Lisp for defining Emacs macros.
这个内核应该强调实现的简单性,但是不能以简化接口为代价.如果这两者产生冲突,问题应该在内核之外被解决.一个原因是内核应该以语言的拓展的形式为其他的系统提供服务,像GNU Emacs使用一个Lisp版本来定义Emacs的宏.
Some aspects of the extreme dynamism of Common Lisp should be reexamined, or at least the tradeoffs reconsidered. For example, how often does a real program do this?
应该重新审视Common Lisp的具有活力的某些方面,或者至少重新考虑权衡。例如:一个真正的程序什么时候会这样做?
1 | (defun f ...) |
Implementations of the next Lisp should not be influenced by previous implementations to make this operation fast, especially at the expense of poor performance of all other function calls.
下一代的Lisp的实现应该被前面的实现影响来使得这种操作变得更快,特别是在性能表现不加的函数调用上.
The language should be segmented into at least four layers:
- The kernel language, which is small and simple to implement. In all cases, the need for dynamic redefinition should be re-examined to determine that support at this level is necessary. I believe nothing in the kernel need be dynamically redefinable.
- A linguistic layer for fleshing out the language. This layer may have some implementational difficulties, and it will probably have dynamic aspects that are too expensive for the kernel but too important to leave out.
- A library. Most of what is in Common Lisp would be in this layer.
- Environmentally provided epilinguistic features.
语言至少要被分成四个方面:
- 内核语言要实现的尽可能的小和简单.在所有情况下,动态重定义的需求应该被重新审视来决定在这一层面上的支持是不是需要的.我相信没有什么是需要在内核层面被重新定义的.
- 充实语言的层面.这个层面也许有一些复杂的实现,并且可能有一些对内核来说代价太大但是又很重要的动态方面的东西.
- 一个lib库.大部分在Common Lisp的功能应该在这个层面
- 在环境上提供其他语言的特性.
In the first layer I include conditionals, function calling, all primitive data structures, macros, single values, and very basic object-oriented support.
在第一个层面上我包括了判断,函数调用,所有基本的数据结构,宏,简单值和非常基本的面向对象的支持.
In the second layer I include multiple values and more elaborate object-oriented support. The second layer is for difficult programming constructs that are too important to leave to environments to provide, but which have sufficient semantic consequences to warrant precise definition. Some forms of redefinition capabilities might reside here.
在第二个层面上我包括了复杂数据和更多的面向对象支持.第二层为了那些很重要以至于脱离环境的复杂的编程结构而提供,但是它也有足够的语义来确保准确的定义.某些形式的重新定义的功能可能存在于此处.
In the third layer I include sequence functions, the elaborate IO functions, and anything else that is simply implemented in the first and possibly the second layers. These functions should be linkable.
第三层我包括了序列函数,IO函数的描述和在第一第二层被简单实现的东西.这些函数要能够被关联.
In the fourth layer I include those capabilities that an environment can and should provide, but which must be standardized. A typical example is defmethod from CLOS. In CLOS, generic functions are made of methods, each method applicable to certain classes. The first layer has a definition form for a complete generic function — that is, for a generic function along with all of its methods, defined in one place (which is how the layer 1 compiler wants to see it). There will also be means of associating a name with the generic function. However, while developing a system, classes will be defined in various places, and it makes sense to be able to see relevant (applicable) methods adjacent to these classes. defmethod is the construct to define methods, and defmethod forms can be placed anywhere amongst other definitional forms.
在第四层我包括了一个环境应该并且可以提供的功能,但是需要被标准化.一个典型的例子就是CLOS中的defmethod.在CLOS中,泛型函数是通过方法来生成的,每一个方法应用来确定一个类.第一层有一个完整的泛型函数的定义形式 — 也就是说,对于泛型函数及其所有方法,在一个地方定义(也就是在第一层编译器想看见的).还有一种方法可以将名称与泛型函数相关联.然而,在开发一个系统的时候,类将被在各个地方被定义,能够在相应的类中看到相应的方法是有意义的.定义方法是用来定义一个方法,并且defmethod可以被放置在任何地方包括其他的一些定义.
But methods are relevant to each class on which the method is specialized, and also to each subclass of those classes. So, where should the unique defmethod form be placed? The environment should allow the programmer to see the method definition in any or all of these places, while the real definition should be in some particular place. That place might as well be in the single generic function definition form, and it is up to the environment to show the defmethod equivalent near relevant classes when required, and to accept as input the source in the form of a defmethod (which it then places in the generic function definition).
但是方法和每一个方法使用的类都相关,也包括每一个类的子类.所以,应该在哪里放置这些defmethod?环境应该允许程序员在任何或者所有的地方看到方法的定义,然而真正的定义应该在一个特定的地方.这个地方可能最好是在单一的泛型函数定义参数里,并且这要由环境来在需要的时候展示等价的定义方法,并且接受输入作为defmethod的参数(然后它放在泛型函数定义中).
We want to standardize the defmethod form, but it is a linguistic feature provided by the environment. Similarly, many uses of elaborate lambda-list syntax, such as keyword arguments, are examples of linguistic support that the environment can provide possibly by using color or other adjuncts to the text.
我们想要标准化defmethod参数,但是它是环境提供的语言特性.同样的,很多使用精心设计的lamdba-list语法,像是键盘参数,是环境可以通过使用颜色或其他文本附件提供的语言支持的示例.
In fact, the area of function-function interfaces should be re-examined to see what sorts of argument naming schemes are needed and in which layer they need to be placed.
事实上,函数-函数接口方面应该被重新考虑:需要什么样的参数命名方案以及需要放置哪个层。
Finally, note that it might be that every layer 2 capability could be provided in a layer 1 implementation by an environment.
最后,需要注意的是每一个第二层的功能也许会在第一层中被提供且在一个环境中实现.
3.7 Help Application Writers Win
The Lisp community has too few application writers. The Lisp vendors need to make sure these application writers win. To do this requires that the parties involved be open about their problems and not adversarial. For example, when an expert system shell company finds problems, it should open up its source code to the Lisp vendor so that both can work towards the common goal of making a faster, smaller, more deliverable product. And the Lisp vendors should do the same.
Lisp社区的应用开发者太少了.Lisp提供者需要保证这些应用开发者能获胜.要做到这一点,要求有关各方公开对待他们的问题,而不是对抗.例如:一个专家系统公司发现了问题,应该开放它的源码给Lisp的提供者这样才能使得大家为了使得Lisp变得更快,更小和更多的交付产品的共同目标努力.Lisp的提供者同样应该这么做.
The business leadership of the AI community seems to have adopted the worst caricature-like traits of business practice: secrecy, mistrust, run-up-the-score competitiveness. We are an industry that has enough common competitors without searching for them among our own ranks.
AI公司的商业领导者似乎采用了最糟糕的漫画式的商业惯例:保密,不信任,提升竞争力.我们是一个有着足够多的公开竞争者的行业,没有在自己的行业中寻找他们.
Sometimes the sun also rises.
太阳照常升起.
总结
- 翻译真的是很痛苦的过程,有些词汇见得少就很难和脑中的中文概念做映射,而且很多词句感觉自己能够看懂但是转成中文还是很困难
- 过程很漫长,跨度甚至快大半个月,虽然期间经历了搬家找工作等等事情,但是写博客能坚持还是很不容易
- 感觉这种形式不是很好,阅读体验上有点缺陷,现在的主题似乎也有一些不适合阅读大篇的文字
- 勉.