跟着qsc搞机(器学习)--线性回归以及最大似然解线性回归问题
开始
在一个普通的周末打开哔哩哔哩刷新动态的时候突然看到qsc投稿了视频的我是表示震惊的!当看到标题是机器学习算法讲堂的时候,我知道:是时候了,是时候开始学一点机器学习了,那么这也算是最近周末的常驻项目之一了.既然看了视频并且手推了一遍,肯定是要搞个大新闻的,那么就开个博客记录一下自己的笔记吧.
先来贴一下qsc视频的地址:
机器学习算法讲堂(2):线性回归推导
机器学习算法讲堂(2.1):最大似然与线性回归
线性回归
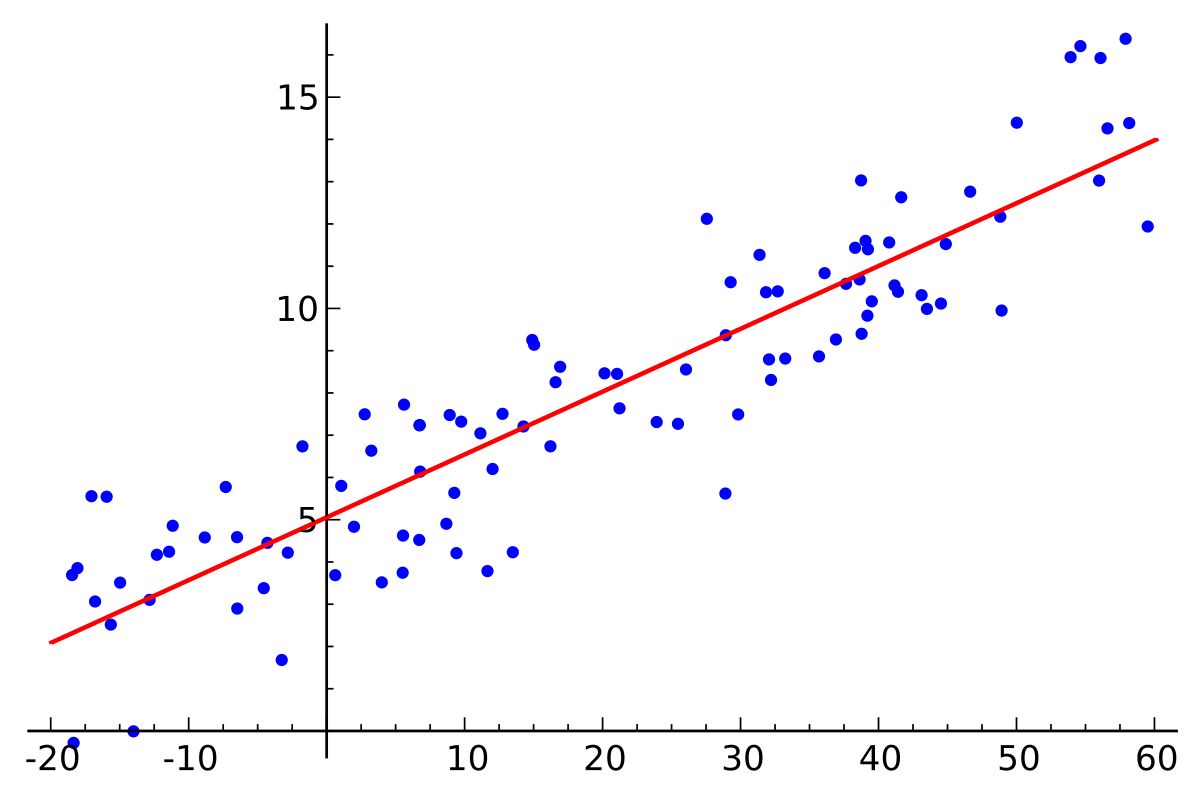
首先允许我再盗一张图:
这是一个非常经典的二维的线性回归的图片.我们的任务就是找到这样一条直线,使得这条直线到平面上所有的点的距离之和最小,写成函数就是这样:
$ f(x)=w_0+w_1x_1+w_2x_2+\cdots=w_nx_n = w^Tx, x\in\mathbb{R}^d,y\in\mathbb{R} $
判断这个函数的好坏我们就定义一个损失函数(loss function)如下(最小二乘法):
$ E=\frac {1} {N}\sum_{i=1}^N(f(x_i)-y_i)^2 $
解释:对每个$x_i$应用预测函数的值f($x_i$)减去数据集中的正确值的差再平方,求1…N所有误差的和再除以N取平均
定义W为使得E最小时的参数:W=argminE,然后我们可以把这个问题转化为求E的导数,找到E的导数为0的点就是E最小的点
先将E化为矩阵的表示形式(这里的x和y都是矩阵的形式):
$$
\begin{split}
E &= \begin{Vmatrix} Xw-y \end{Vmatrix}^2 \\
&=(Xw-y)^T(Xw-y)
\end{split}
$$
接下来对E求导(左导右不导加上右导左不导):
$$
\begin{split}
dE&= (Xdw)^T(Xw-y)+(Xw-y)^TXdw \\
&=2(Xw-y)^TXdw \\
\frac {dE^T} {dw}&=(2(Xw-y)^TX)^T \\
&=2X^T(Xw-y) \Rightarrow \nabla
\end{split}
$$
我们可以把$\nabla$当做是训练的梯度,当$2X^T(Xw-y)=0$的时候w可以取到最小,转换一下:
$w=(X^TX)^{-1}X^Ty$
当$X^TX$可逆的时候就可以直接求解,不可逆的时候就需要使用梯度下降的方法来训练使得E收敛到最小获得w的值.
梯度下降:$w(t+1)=w(t)-\lambda\nabla$,$\lambda$为梯度下降的步长.
最大似然
还是回到上面的图片中,在我们用函数来拟合这组数据的时候,因为无法完美的拟合数据,所以我们假设有我们没有观察到的因素存在导致我们的拟合函数存在误差,而这个拟合函数所缺失的不可解释的那部分误差就是直线到数据点之间的距离.
同时我们换个角度来看这个数据集,既然这些点被我们观测到了,就说明这些点被我们观测到的概率是最大的,由此可以推出,我们可以寻找一个函数,使得我们能够观测到这些点的概率最大,那我们也就找到了对些数据最好的拟合.
似然函数推导
假定存在一个数据集D=$\lbrace(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)\rbrace$
我们定义函数$y_i=f(x_i)+\varepsilon_i,\varepsilon_i为不能完全解释的误差$
问题就转化成了:现在我们有N个f(x)函数,我们要评估哪个模型最有可能产生这一组数据,用概率来表示就是:
$P(D|x,\theta)=P(y_1,y_2,y_3,\cdots,y_N|x_1,x_2,x_3,\cdots,x_N,\theta)$
假设数据之间是相互独立的(概率相乘):
$P(y_1,y_2,y_3,\cdots,y_N|x_1,x_2,x_3,\cdots,x_N,\theta)=\prod_{j=1}^N P(y_j|x_j,\theta)$
我们的似然函数也就是:$likelihood(\theta)=\prod_{j=1}^N P(y_j|x_j,\theta)$
因为对于数据集D来说x,y已经确定所以可以将概率转换如下:
$P(y_i|x_i,\theta)=P(y_i|f(x_i)+E)=P(y_i-f(x_i)|E)$
可以看到:对于任意的x,y来说概率就和模型的预测值和实际值之间的误差和E的分布相关了.
最大似然和线性回归
根据我们之前的定义:$y_i=f(x_i)+\varepsilon_i$ 我们可以推出:$\varepsilon_i=y_i-w^Tx_i$ (也就是前面线性回归推导中使用的误差)
我们假设Y服从均值为$w^Tx$ ,方差为1的分布:
$$
P(Y|x)=P(\varepsilon|x)=\frac {1} {\sqrt{2\pi}\times e^{\frac {-\varepsilon^2} {2}}}
$$
将上面的$\varepsilon_i=y_i-w^Tx_i$ 代入公式:
$$
P(Y|x)=P(\varepsilon|x)=\frac {1} {\sqrt{2\pi}\times e^{\frac {-(y_i-w^Tx_i)^2} {2}}}
$$
由于误差符合正态分布,我们将概率代入似然函数中并且对似然函数取log:
$$
likelihood(\theta)=\log \prod_{j=1}^N \frac {1} {\sqrt{2\pi}\times e^{\frac {-(y_i-w^Tx_i)^2} {2}}}
$$
化简得到:
$$
N\log(\frac {1} {\sqrt{2\pi}})+\frac {\sum_{i=1}^N-(y_i-w^Tx_i)^2} {2}
$$
去掉前面的常数项和后面的常系数之后可以化简为:
$$\sum_{i=1}^N-(y_i-w^Tx_i)^2$$
我们要使得概率最大也就是使得似然函数最大:
$$max\sum_{i=1}^N-(y_i-w^Tx_i)^2$$
也就是(去掉负号):
$$min\sum_{i=1}^N(y_i-w^Tx_i)^2$$
完成!是不是发现这和最小二乘法给出的公式(loss function)是一样的?因为最小二乘法是最大似然解法的一种特殊情况.
从最大似然解法的推导中我们可以看到:均方误差最小化求解线性回归和假设预测符合高斯分布然后利用最大似然估计求解线性回归得到的结果是相同的
总结
虽然是最简单的线性回归的推导,但是从概率的角度利用最大似然来推出loss function的那一刻还是感觉到:数学真炫酷啊~
之前看机器学习的时候感觉数学公式看到就很头疼,但是现在自己硬着头皮推一遍之后发现并没有那么复杂而且通过这种硬盒的方式来学机器学习的算法是获益匪浅.最后再说一句:qsc的视频我是期期都看啊~