不动点,递归,二进制--奇妙的分形三角形

发表于 更新于 分类于

我看到了它，却不敢相信它.—by康托尔

前言

这是一个我想写了很久的话题,但是却迟迟没有开始,因为这个话题过于艰深而且涉及的知识面已经超出了我的边际,然而在这几周重读了递归之后还是打算将其记录下来,记录下这令人神往着迷的美妙的数学世界的经历.

标题很自大地致敬了**哥德尔、艾舍尔、巴赫–集异璧之大成**这本刷新我认知的奇书

**康托尔、哥德尔、图灵——永恒的金色对角线**这篇我非常喜欢的关于不动点的博客.

从递归说起

递归,这个编程中基础到不能再基础的知识点,却在我开始学习SICP之后一次次刷新着我的编程观,大道化简,即便是这样一个在认知中基础得不能再基础的编程方式也以其独特的魅力向我们展示着编程和数学中隐藏着的深刻而绮丽的美丽之处.

汉诺塔

这是一个几乎每个学习编程的人都会学到的关于递归的最好的例子,在此就不再详述这个问题的介绍了,维基百科链接在这里.

给出移动的流程:

1
2
3
4
移动4个盘子=
    移动3个盘子到B
    移动最大的盘子到C
    移动3个盘子到C

下面给出python版本的解法:

1
2
3
4
5
6
def solve_toh(n_disks):
    if n_disks == 0:
        return
    solve_toh(n_disks-1)
    move_disk(n_disks-1)
    solve_toh(n_disks-1)

这个凝聚了大量的智力劳动的问题却以其极简的表达形式展示了出来而且是这么的容易被理解,这也是递归的魅力所在吧.

二进制

下面我们引入二进制,当然这也是非常基础的计算机知识了,但是这里我们需要关注的是它的计数规律:

1
2
3
4
数出二进制1111=
    数出二进制0111:     0111
    将首位置1,后三位恢复:1000
    数出二进制0111:     1111

可以看到的是,这个过程是非常递归的一个过程,1111需要先数0111而0111需要先数0011…..那么这和汉诺塔有什么关系呢?让我们这样来考虑问题:

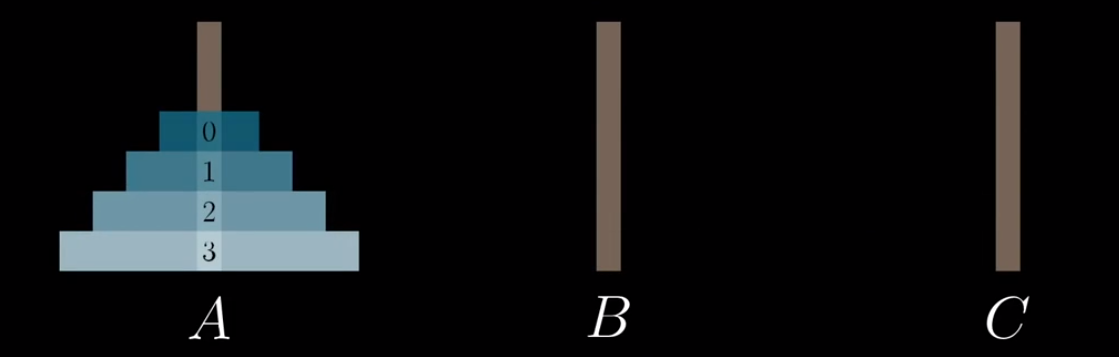
我们将A柱子上的4个盘子记为一个4位二进制数,它的起始状态就是0000,然后我们开始计数:0001,0010,0011….而每次某个二进制位变成1的时候,就将对应的盘子向右移动一个柱子(到最左的话就移动到A),如:0001就是将编号为0的盘右移到B:

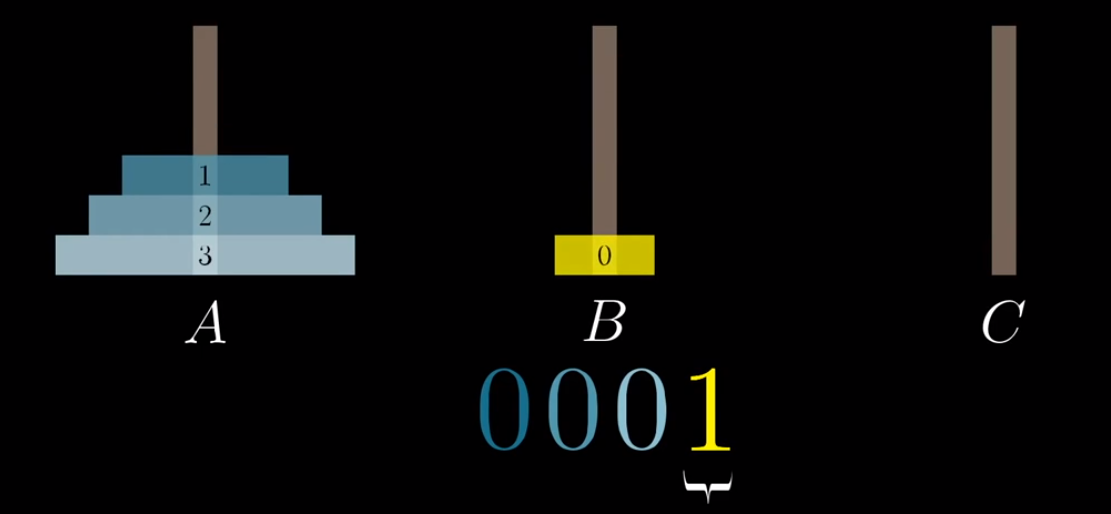
然后如此循环,我们就可以解决汉诺塔问题.当我看到这里的时候我是很惊异的,这难道只是一个巧合吗?我们来观察一下上面的2段代码:

1
2
3
4
5
6
7
solve_toh(n_disks-1)
move_disk(n_disks-1)
solve_toh(n_disks-1)

数出二进制0111:     0111
将首位置1,后三位恢复:1000
数出二进制0111:     1111

正好一一对应,不是吗?

也就是说,移动编号为1的盘子,需要移动0号盘子2^1-1=1下,而移动2号盘子需要移动0号和1号盘子总共2^2-1=3下,而3下中也是0号2下,1号1下,明显的是:二进制数字变化是递归的且和每个盘的变化是一一对应的.

还是递归

匿名递归

在SICP第一章中我们就了解到,我们可以将求根的函数和寻找一个函数的不动点结合起来,只要这个函数在迭代的过程中是收敛的,比如(其中的fixed-point就是寻找不动点的函数):

1
2
3
4
5
(define (f x)
    (/ 2(+ x (/ x 2))))

(define (sqrt x)
    (fixed-point f 1))

在维基百科的定义中,函数的不动点就是x=f(x)的点,但是这对于递归有什么意义呢?我们这样来思考问题:写一个lamdba表达式来实现递归求解阶乘.

阶乘

那么就先把函数给写出来:

1
lamdba n: n==0?1,self*(n-1)

这里的self就是这个函数的名称,在不使用匿名函数的时候,固然是很简单的,直接将函数名填进去就行了,但是lamdba就不行了,因为在函数被定义之前它是没有名字的.既然我们不能直接填入函数名,那么就将其参数化:

1
lamdba self,n: n==0?1,self*(n-1)

然后我们给他加一个名字:

1
let P = lamdba self,n: n==0?1,self*(n-1)

观察这个函数我们可以发现,如果调用P的时候,我们传一个真正的阶乘函数进去,那么P(power, 10)就可以正确的求解阶乘了.恩?但是我们不就是在找一个阶乘函数吗?虽然有这样的疑惑,但是还是先写一个出来再说嘛:

1
power(n) = n==0? 1,n*power(n-1)

然后我们靠柯里把这个函数变成这样:P(power),也就是说这个函数还等待接收一个数字就能求出对应的阶乘了.恩?等等,这个power也不行啊,这也是个不存在的函数啊!那么别急,先展开一下:

1
P(power) = n==0?1,power(n-1)

恩?这不就是power的定义吗,what?是的,P(power)=power了!,这是什么,这不就是函数的不动点吗!也就是说,对于伪递归函数P,存在一个点power使得P(power)=power,那么问题就变成了,我们要找到一个工具,只要对P用一下这个工具,我们就能获得power,power是什么?power可是一个真正的递归函数啊,那么这个问题就解决了.也就是说:找到一个函数Y,使得Y(P)=power:

1
2
3
4
Y(P)=power
因为:P(power)=power
所以:Y(P)=power=P(power)=P(Y(P))
也就是说:Y(P)=P(Y(P))

那么问题就变成了寻找这个Y,似乎问题到了这里也没有丝毫推进但是只要得到Y,那么这就是一个银弹可以对任何一个函数使用,就可以得到其真正的递归函数.让我们回到

1
let P = lamdba self,n: n==0?1,self*(n-1)

如果我们调用P(P,3)会得到:

1
3==0?1,P(3-1)

发现并不能继续循环调用下去,那么我们调整一下P函数:

1
let P = lamdba self,n: n==0?1,self*(self, n-1)

那么上面的调用就会变成:

1
3==0?1,P(P,3-1) ==> P(P,2)

诶?这不是就搞定了吗,那我们绕这么远的路还要寻找Y干嘛呢?我们将这个思想代入到Y中:

1
2
3
let Y = lambda F: 
    let f= lambda self: F(self(self))
    return f(f)

用P代入:

1
2
3
4
5
6
7
8
9
Y(P):
    let f = lamdba self: P(self(self))
    return f(f)
也就是:
Y(P)=f(f)
而f(f)根据定义可以得到:
f(f)=P(f(f))
也就是:
Y(P)=f(f)=P(f(f))

将其代回P函数中:

1
2
3
P(f(f)) = lambda: n==0?1,n*P(f(f))(n-1)
假设P(f(f))=fib,那么:
fib = lambda: n==0?1,n*fib(n-1)

终于得到了一个完美的阶乘函数!而这个Y不是别的,就是Y组合子.也就是说,只要使用Y组合子这个神奇的函数,我们就可以获得所有函数的递归形式.

我们赋予了函数式编程能够表达递归的能力

下面给出一个python的实现:

1
2
def y_combinator(f):
    return (lambda u: u(u))(lambda x: f(lambda *args: x(x)(*args)))

那么匿名的阶乘函数就如下:

1
y_combinator(lambda fab: lambda n: 1 if n < 2 else n * fab(n-1))(10)

在SICP的课程开始,老师说过:如果我们想要操纵一个精灵(函数)只要能够叫出它的名字就可以,而有了Y组合子的帮助,我们能够操纵一大类叫做匿名函数的精灵了.

Congratulations!你已经正式加入了Lisp邪教!这是会徽:

递归艺术

爱舍尔有一副很有名的画–画手,这也是一个将递归在绘画艺术中发挥到极致的画家了.

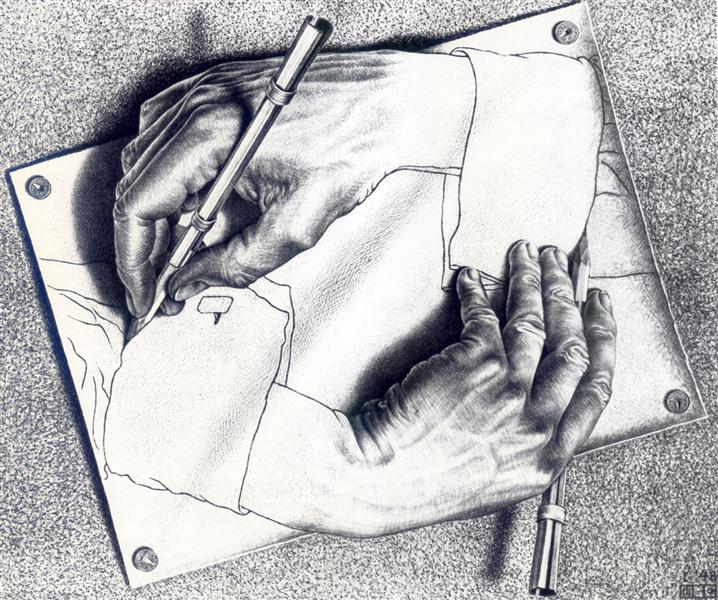
可以看到这也是一个很递归的过程,而在SICP的第四章中,eval和apply就像是图上的两只手,在互相描绘着对方.

我们可以让一个程序输出它本身吗?下面给出一个js的实现和一个python的实现:

1
(function (s) { console.log( '(' + s + ')(' + s + ')' )})(function (s) { console.log( '(' + s + ')(' + s + ')' )})
1
print(lambda x:x+`(x,)`)('print(lambda x:x+`(x,)`)',)

递归分形

在SICP第二章中,我们使用Lisp来实现过一个能够画出递归的图片的语言,效果如下:

还有一种分形的图形叫做谢尔宾斯基三角形

一种递归的实现方法是每次连接一个三角形的三条边的中点,然后对所有的三角形重复这个过程.伪代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def sierpinski(points,degree):
   drawTriangle(points)
    if degree > 0:
        sierpinski([points[0],
                        getMid(points[0],points[1]),
                        getMid(points[0],points[2])],
                   degree-1)
        sierpinski([points[1],
                        getMid(points[0],points[1]),
                        getMid(points[1],points[2])],
                   degree-1)
        sierpinski([points[2],
                        getMid(points[2],points[1]),
                        getMid(points[0],points[2])],
                   degree-1)

还是汉诺塔

(你说的是三角形,关我汉诺塔什么事?)

我们来改变一下移动汉诺塔的策略,每次移动的时候只能把圆盘移动到相邻的柱子上,改变了策略之后会发生什么呢?我们来假设移动一下4个盘子:

1
2
3
4
5
6
7
移动4个盘子=
    移动3个盘子到C
    移动最大的盘子到B
    移动3个盘子到A
    移动最大的盘子到C
    移动三个盘子到B
    移动三个盘子到C

如果这时候我们还要保持每一位数的变化和对应盘子的移动的话,可以看一下上面的流程:

1
2
3
4
移动4个盘子=
    移动3个盘子到B
    移动最大的盘子到C
    移动3个盘子到C

很自然的可以想到,因为每次都多移动了一下,那么使用三进制怎么样?right

这时候事情就变得有趣了起来,让我们想一下:4个盘子进行移动一共移动多少下?3^4=81次.4个盘子总共可以产生的不重复的盘子分布状态是几种?

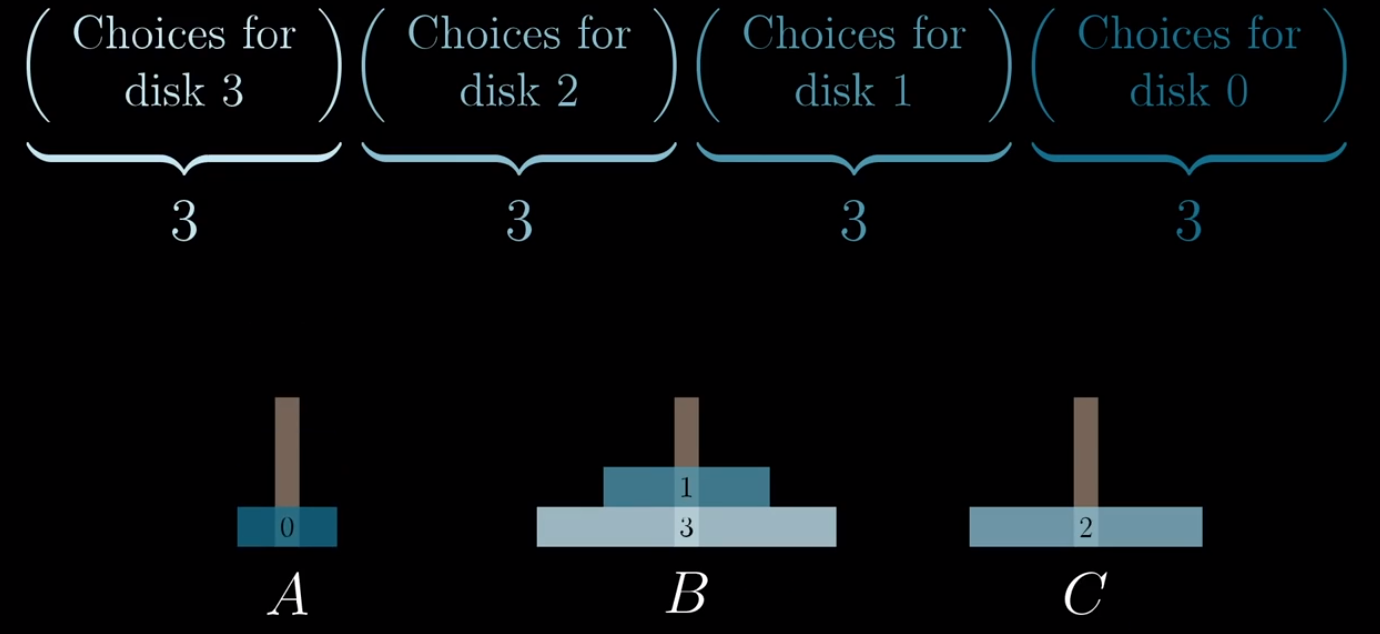
3*3*3*3=81种,这是巧合吗?也就是说,上面按照三进制的走法就是最优解了(因为如果前后有重复的状态的话,中间的步骤就可以被省略了),事情变得非常有趣了起来.

我们把所有可能的盘子状态按照两个直接可以一步做到的方式连在一起,例如(0号盘可以相互一步到达):

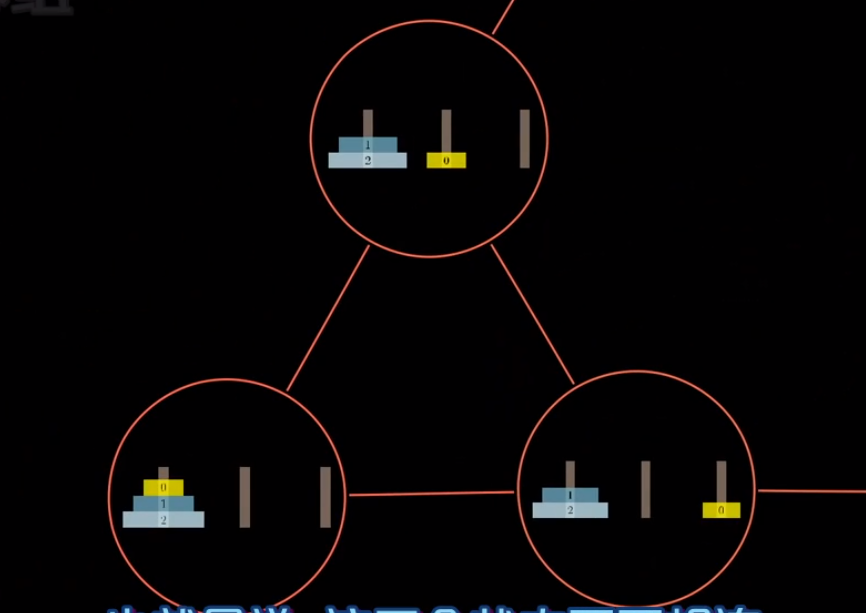
这样把全部的盘面都连接在一起的话:

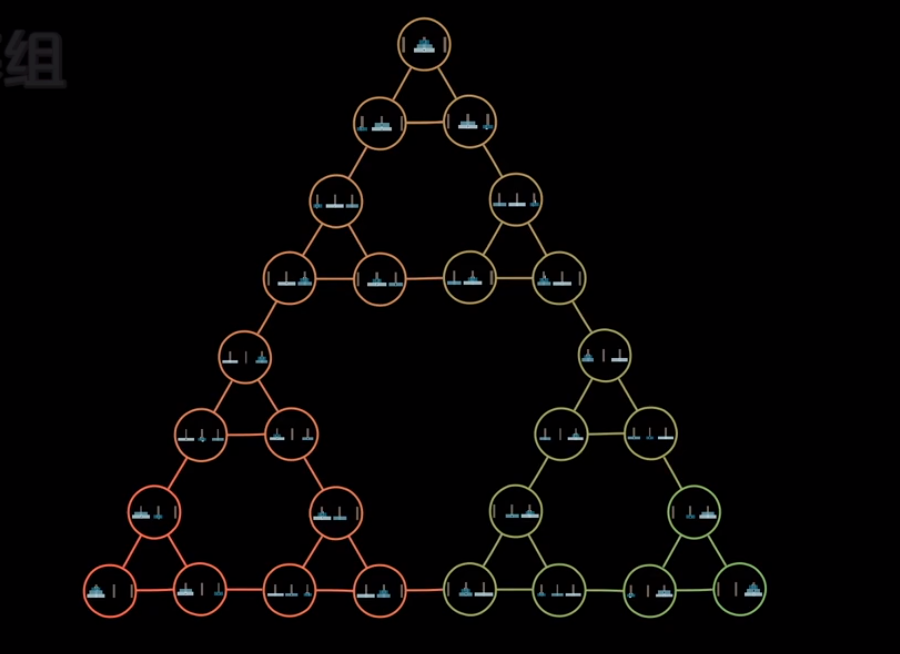
恩?这是什么?这不是谢尔宾斯基三角形嘛

虽然难以置信,但是事情就是这样发生了

是的,虽然大家平时完全不见面,但是通过递归使得分形和汉诺塔联系在了一起.

当你一旦发现了数学中的某些规律在你的知识的每个角落都散发着光芒的时候,这将你深深吸引的绚丽的光芒就将指引着你去寻找更多美丽的存在. —by沃·兹基硕德

那么最优解呢?最优解也是可以找到的

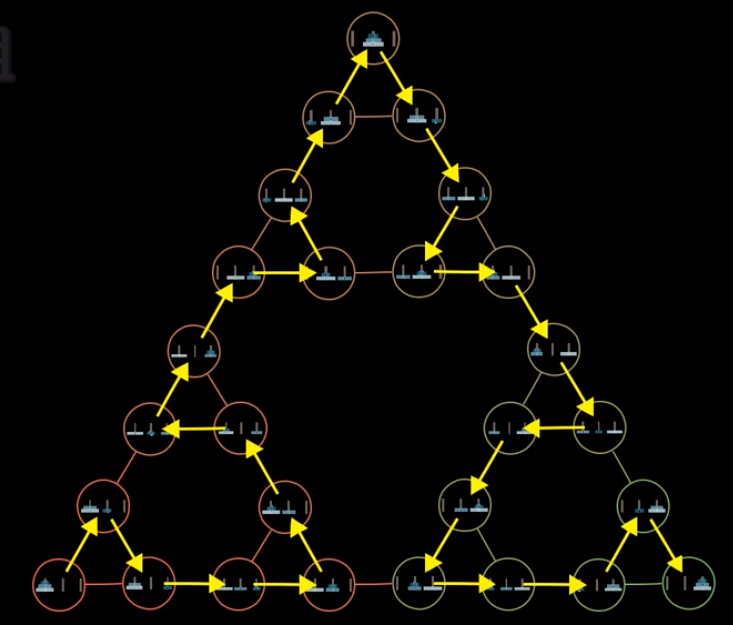
看到这里,相信没有人会不感叹数学之美以及这递归中的种种巧合与联系.

总结

总感觉意犹未尽但是又说不出来,写完也总是不能令自己满意,但是总也不写的话就会一直惦记着,就先把想到的写出来要是以后还有再继续补充罢.

关于Y组合子和停机问题以及哥德尔不完备定理的内容还是参见康托尔、哥德尔、图灵——永恒的金色对角线这篇文章和哥德尔、艾舍尔、巴赫–集异璧之大成这本书,这里空白太小写不下.

引用

用二进制来解汉诺塔问题

隐藏在汉诺塔中的分形曲线

康托尔、哥德尔、图灵——永恒的金色对角线

谢尔宾斯基三角形能用编程写出来么？该怎么写？

10种编程语言实现Y组合子

python数据结构与算法 23 宾斯基三角形

谈谈递归

Quine 是什么