跟着qsc搞机(器学习)--从赌博机到推荐系统

发表于 更新于 分类于

在度过了今年的最爽假期也是最后假期之后的星期六,又看到了qsc更新视频的我是很欣喜的,但是看完之后的我是懵逼的:怎么难度一下从天堂到了地狱~~,当然了,最后卿学姐也说了,这是一个导论性质的介绍,那么就让我再总结一下吧.

先放上视频的地址:机器学习算法讲堂(4):Explore and exploit算法 LinUcb《Bandits in Recommendation》

从老虎机开始

让我们来想象这样一个情景:

一个赌徒，要去摇老虎机，走进赌场一看，一排老虎机，外表一模一样，但是每个老虎机吐钱的概率可不一样，他不知道每个老虎机吐钱的概率分布是什么，那么每次该选择哪个老虎机可以做到最大化收益呢？

这就是多臂赌博机问题(Multi-armed bandit problem, K-armed bandit problem, MAB),也就是我们需要在有限的回合内找出一个系统的最大收益,而之所以用MAB问题来举例的原因也是因为,这个问题的抽象可以套在很多推荐系统的问题之上,例如:

  • 假设一个用户对不同类别的内容感兴趣程度不同，那么我们的推荐系统初次见到这个用户时，怎么快速地知道他对每类内容的感兴趣程度？
  • 假设我们有若干广告库存，怎么知道该给每个用户展示哪个广告，从而获得最大的点击收益？是每次都挑效果最好那个么？那么新广告如何才有出头之日？
  • ….

可以发现,这些问题都跟老虎机是一样的:我们需要在有限的回合内找到老虎机的最大收益==>我们需要在有限次数内找到推荐广告的最大收益

而在推荐系统领域对于这类问题有一个统一的说法,叫做Explore-Exploit问题,也就是如何来最大化探索和利用的价值的问题,比如:

  • Explore(探索):我们需要探索用户的兴趣点而且需要不断地探索新的兴趣来保证用户对系统的新鲜度,这是一个长期的,挖掘潜在价值的,成长型的需求
  • Exploit(利用):当我们探索出最大价值的时候我们需要利用,这是一个贪婪的,短期的,需要奖励来反馈激励的需求

就像是在玩老虎机:我们发现一个老虎机吐钱很多,那肯定需要用它来赚钱啊,但是我们也不能保证它就是最赚钱的,我们也得去探索其他的老虎机的赚钱能力,而如何来协调探索和利用的关系来使得我们的系统产生出最大的价值,也就是需要研究的地方了.

Bandits in Recommendation

知识准备-累积遗憾

当然这一点在qsc的视频中没有着重讲,但是在看其他博客的时候还是觉得需要补充一下.

累积遗憾也就是Bandits算法中用来量化一个策略好坏的指标,用公式写出来是这样的:
$$
R_A(T) = E\left[\sum_{t=1}^Tr_t,a_t^*\right]-E\left[\sum_{t=1}^Tr_t,a_t\right]
$$

这里t表示轮数,r表示回报.公式右边的第一项表示第t轮的期望最大收益，而右边的第二项表示当前选择的arm获取的收益，把每次差距累加起来就是总的遗憾.显然的,累积遗憾越小,算法的效果也就越好.

$\epsilon$-greedy algorithm(贪心策略)

我们来看一种最简单的贪心的策略,方法如下:
在每一步:

  • 使用一个我们选择的概率$\epsilon$,随机的选择一个手臂去摇老虎机(探索)
  • 其他的(1-$\epsilon$)概率下,我们选择当前最赚钱的老虎机摇一下(利用)

然后我们观察最后的回报来调整概率达到最优解,然而这个算法的问题在于:我们的选择是随机的,但是实际上,我们在摇了很多下老虎机之后是知道哪些比较赚钱那些不怎么赚钱,而这个信息没有被利用起来.我们的改进思路也就变成了从随机选择去寻找更加聪明的选择方法.

Thompson sampling

Beta Distribution(Beta分布)

关于beta分布几乎是没有了解的,但是在这只需要知道它是一种概率分布就可以了,这里先给出分布的公式:
$$
f(x;\alpha,\beta) = constant \cdot x^{\alpha-1}(1-x)^{\beta-1}=\frac {1} {B(\alpha,\beta)} x^{\alpha-1}(1-x)^{\beta-1}
$$

这里我们需要关注的是beta分布的方差的计算(实验的次数越少方差就越大):
$$
var(X)=E[(X-\mu)^2]=\frac {\alpha\beta} {(\alpha+\beta)^2(\alpha+\beta+1)}
$$

算法解释

而这个方差的特征正是我们所希望的,比如我们摇了一个老虎机10000次,它赚的钱是500块而另一个老虎机我们只摇了100次赚的钱是5块,如果我们在这两个老虎机之间做抉择的话,肯定会选择后一个,因为它的上限比前者高,因为前者我们几乎以及可以肯定它就是10000次赚500,而后者可能比它更赚钱,虽然现在来看它们的平均收益是一样的.下面是ppt中对beta分布的可视化:

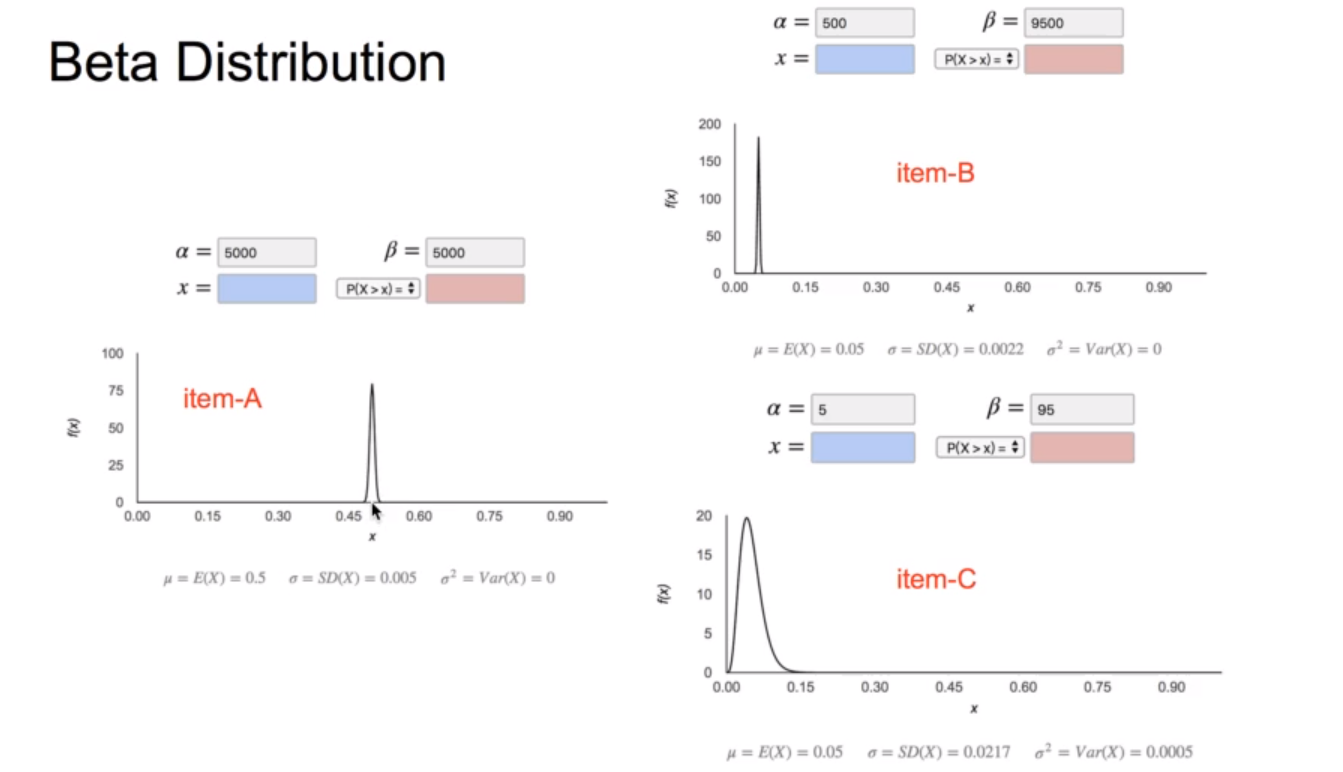
item-b和item-c就是上面的摇了10000次的老虎机和摇了100次的老虎机.
而Thompson sampling算法的思路就和上面的想法一样,假设每个老虎机的吐钱概率符合beta分布,跟随机选择手臂的贪心算法比起来,优化的地方就在于:用每个手臂的beta分布生成一个随机数,选择这些随机数中最大的那个手臂摇一下.下面给出贪心算法和Thompson sampling算法伪代码的比较:

UCB:Upper Confidence Bound(置信区间上界)

在之前我们也提到了,贪心算法的缺点就在于没有利用前面已经摇了的老虎机的信息,上面的Thompson sampling算法给出了一种利用的思路,而UCB(置信区间上界)则是另一种利用的方式.
大致的思路是:我们假设每一个老虎机的吐钱概率
$$
Q(a)\leq \hat{Q_t}(a)+\hat{U_t}(a)
$$
这里的$\hat{Q_t}(a)$就是每个老虎的收益的均值,而$\hat{U_t}(a)$可以认为是这个老虎机的赚钱潜力,而这个潜力也能够使得很少被摇到的但是很赚钱的老虎机被发掘出来.那么现在的问题就是要对$\hat{U_t}(a)$来确定一个上界,也就是它的极限赚钱能力是多少,而这个上界在1963年被Hoeffding找到了并且命名为Hoeffding Inequality,其中的上界的解是:
$$
\hat{U_t}(a) = \sqrt{\frac {-\log p} {2N_t(a)}}
$$
其中的p是我们假设的概率,$N_t(a)$则是实验的次数

Bayesian UCB

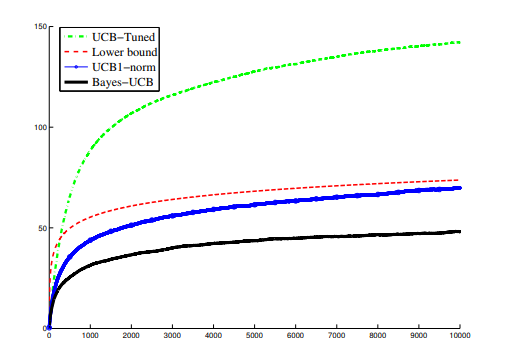
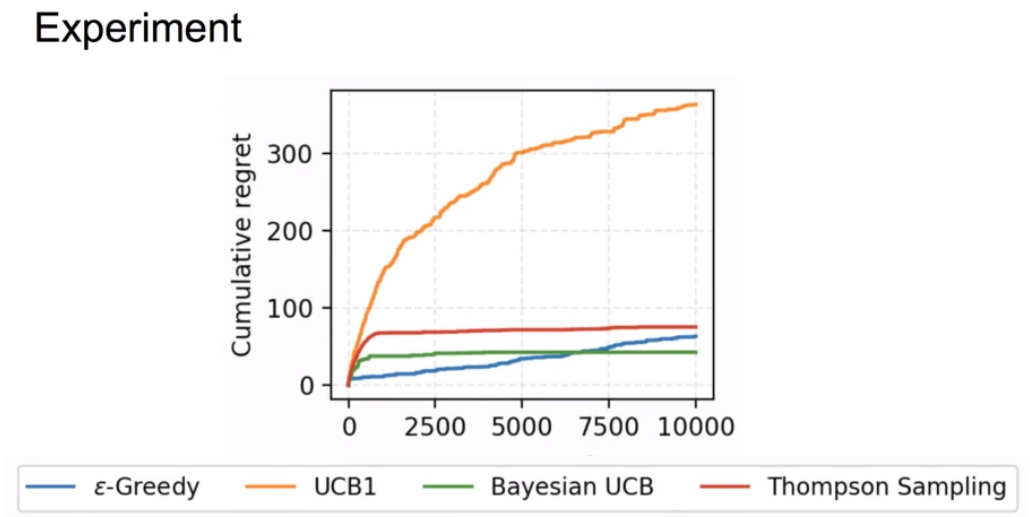
虽然我们已经可以通过上面的公式来计算每个老虎机的置信区间上界从而选择摇那个老虎机,但是缺陷是这个上界太大了,也就是说实际的效果并不会很好,而其中的一个解决方案就是假设$Q(a)$服从贝叶斯分布,这样我们就可以直接根据公式来算出上界,至于效果的话,直接引用paper中的一个比较,可以看到优化的效果是比较好的.

这是上面提到的几种算法的效果的比较图:

LinUCB–UCB算法的一次进化

算法的优化还在继续,上面的UCB算法的最大问题在于它是context-free(上下文无关)的,这怎么行呢(滑稽),所以我们的算法优化的下一步就是给UCB算法插上特征的翅膀.也就是我们给每一个手臂都加上一个上下文的特征,当然这里再举老虎机似乎不是很贴切了,可以把手臂变成替用户挑选商品的手臂.那么与此对应的,我们给每个手臂能够获得的期望收益一个定义:
$$
E[r_{t,a}|x_{t,a}] = x_{t,a}^\top \bf {\theta}_{a\cdot}^*
$$
假设手机到了m次反馈，特征向量可以写作Da(维度为md)，假设我们收到的反馈为Ca(维度为m1)，那么通过求解下面的loss，我们可以得到当前每个手臂的参数的最优解：
$$
loss = (C_a-D_a\theta_a)^2+\lambda\begin{Vmatrix} \theta_a \end{Vmatrix}
$$
然后我们可以使用ridge-regression(岭回归)得到explicit solution(闭式解):
$$
\theta_a = (D_a^TD_a+I)^-1D_a^Tc_a
$$
而根据UCB方法,我们除了需要一个均值之外,还需要找到一个置信上界,而这个置信上界也被人找出来了.反正最后我们需要训练的函数就可以确定下来,就是下面这一坨了(实在不行了,mathjax真难写):

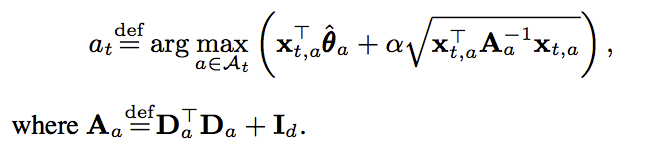
给出LinUCB算法的伪代码:

优点

  • 是上下文相关的
  • 上下文特征的回报函数是线性的
  • 是一个岭回归==>是有解析解的
  • 服从高斯分布==>有UCB上界
  • 是一个在线的算法(个人认为是:有新的数据进来不需要重新训练模型)

优化方向

下面就是一些比较简短的优化的方向了

  • CoLin:协同过滤,引入了用户之间的关系(这个还是挺重要的特征)
  • hLinUCB:加入了hidden-feature(隐向量)
  • FactorUCB=hLinUCB+CoLin

最后的最后,放上一个Bandit算法的进化路径的图吧:

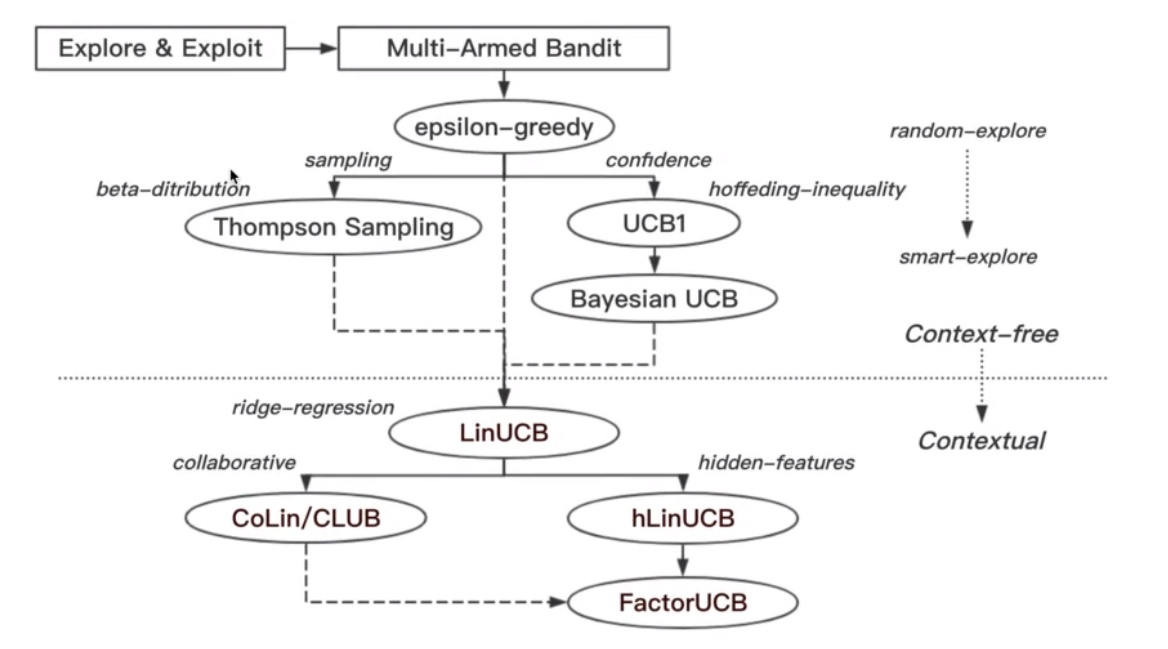可以看到进化的方向就是从随机选择到更加聪明的选择,从上下文无关到上下文相关,也是越来越能够贴近推荐系统的核心需求了.

参考博客

专治选择困难症——bandit算法
UCB算法升职记——LinUCB算法
推荐系统遇上深度学习(十三)–linUCB方法浅析及实现
推荐系统遇上深度学习(十二)–推荐系统中的EE问题及基本Bandit算法

论文引用

LinUCB
CoLinUCB
CLUB
hLinUCB
FactorUCB

总结

因为是一个导论性质的小讲堂所有内容还是有点多的,消化起来也有点慢也有点吃力,但是还是很开拓眼界的.

吾尝终日而思矣,不如须臾之所学也