优点

开始

我们首先从线性回归解法的角度来看一个特征组合的问题,如果现在数据涉及到训练集中的两个特征,那么LR就要写成:

可以看到在这个方程中,随着特征选取的数量变多,特征组合之后的复杂度是特征数量个N相乘,这是在训练过程中不能接受的,并且线性回归的方法只能在不为0的情况下进行训练,对于稀疏的数据来说训练是不充分的.而FM解决的就是LR复杂度过高和对稀疏数据训练不充分的缺点.

FM的思路就是将W分解为,这也就是FM名字的由来,等于是因式分解W.接下来是FM的推导的过程:
首先引入辅助变量

已知特征矩阵W为:

Misplaced &\\begin{pmatrix} w_{11} & w_{12} & w_{13} & \\cdots & w_{1n} \\\ w_{21} & w_{22} & w_{23} & \\cdots & w_{2n} \\\ \\vdots & \\vdots & \\vdots & \\ddots & \\vdots \\\ w_{n1} & w_{n2} & w_{n3} & \\cdots & w_{nn} \\\ \\end{pmatrix}

V矩阵为:

Misplaced &\\begin{pmatrix} v_{11} & v_{12} & v_{13} & \\cdots & v_{1k} \\\ v_{21} & v_{22} & v_{23} & \\cdots & v_{2k} \\\ \\vdots & \\vdots & \\vdots & \\ddots & \\vdots \\\ v_{n1} & v_{n2} & v_{n3} & \\cdots & v_{nk} \\\ \\end{pmatrix}

且有结论:当k足够大时,对于任意对称正定实矩阵,均存在实矩阵使得

这样一来,我们只要找到一个就可以解决这个问题了,而分解成的优势在于有效的降低了算法的复杂度,下面是对FM算法的求解:

根据上面的分解,可以将FM公式写为:

这里主要需要求解的就是最后一项:

Misplaced &\\begin{split} &\\sum_{i=1}^{n-1}\\sum_{j=i+1}^n<v\_i,v\_j>x\_ix\_j \\\ =&\\frac {1} {2}\\sum_{i=1}^n\\sum_{j=1}^n<v\_i,v\_j>-\\frac {1} {2}\\sum_{i=1}^n<v\_i,v\_i>x\_ix\_i \\text{，把j化成i,需要减去重复的部分} \\\ =&\\frac {1} {2} \\left( \\sum_{i=1}^n\\sum_{j=1}^n\\sum_{f=1}^kv_{i,f}v_{j,f}x\_ix\_j-\\sum_{i=1}^n\\sum_{f=1}^kv_{i,f}v_{i,f}x\_ix\_i \\right) \\text{,把上面的等式代入进来} \\\ =&\\frac {1} {2} \\sum_{f=1}^k \\left( \\left( \\sum_{i=1}^nv_{i,f}x\_i \\right) \\left( \\sum\_{j=1}^nv_{j,f}x\_j \\right)-\\sum\_{i=1}^nv_{i,f}^2x\_i^2 \\right) \\text{,提出公共的求和部分} \\\ =&\\frac {1}{2} \\sum\_{f=1}^k \\left( \\left( \\sum_{i=1}^nv_{i,f}x\_i \\right)^2-\\sum\_{i=1}^nv_{i,f}^2x_i^2 \\right) \\text{,前面2项除了下标的i,j不同之外是一样的,所以合并} \\\ \\end{split}

我们可以看到公式化简到最后,复杂度就只和求和符号上的k,n相关了,所以复杂度可以简单的记为O(nk),但是这已经比之前的线性回归的解法复杂度低了很多了,这可以视为是线性的复杂度.

下面看一下FM的梯度的计算,我们对分别求偏导可以写为:

Misplaced &\\frac {dy} {d\\theta}= \\begin{cases} 1, & \\text{if $\\theta=w\_0$} \\\ x\_i, & \\text{if $\\theta=w\_i$} \\\ x\_i\\sum_{j=1,j\\neq i}^nv_{j,f}x\_j & \\text{if $\\theta=v\_{i,f}$} \\\ \\end{cases}

最后一个公式可以化为:

我们可以看到这个梯度计算的公式中,计算复杂度也只和n相关也就是说:复杂度是O(n)!相比于简单的LR动不动的N方的复杂度来说,FM的复杂度可以说是相当的低了.

这里就只是先列举一下FM的一些拓展使用:

下面就放几个图片吧(这次是自己截图放的图床)
DeepFM:

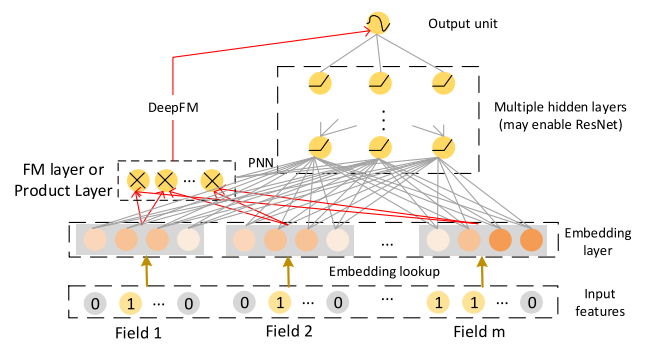
xDeepFM:

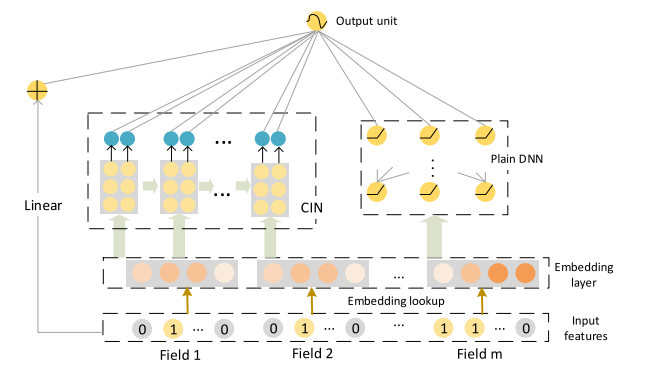
贴一下论文的地址:
Factorization Machines