前言
实习之后感觉节奏和学校还是有些变化的,不知不觉俩月也过去了,SICP却才开始第二章的总结,需要督促自己了.
第二章主要是:
- 复杂数据的抽象
- 数据导向编程
- 数据类型闭包
- 符号表达式处理(引用)
现在到了数学抽象中最关键的一步:让我们忘记这些符号所表示的对象.
(数学家)不应该在这里停步,有许多操作可以应用于这些符号,而根本不用考虑它们到底代表着什么东西.
——Hermann Weyl,思维的数学方式
总结
数据抽象
- 数据抽象可以使我们从构造对象的细节中脱离出来而使用一些基本的数据对象来完成对复杂对象的操作.
- 数据抽象的基本观点就是使用抽象的数据来构造复杂的数据对象.
- 抽象数据之间的接口通过_selectors_和_constructors_来实现
- 构造抽象数据的一个有力的方法就是_closure_(闭包)
Pairs(序对)
pairs可以说是Lisp中所有的数据结构的基石了,而Lisp中的pairs相比C++或者Java有着更强大的能力,因为它是closure的,可以创造出无限复杂的数据结构出来.更重要的一点是,从pairs出发,_数据和过程的边界_也变得越来越模糊了,在SICP课程中教授也是从pairs出发,模糊了数据和过程的边界.
从虚无中创造出数据
这是教授上课时讲的,我们可以从虚无中创造出数据,例子如下(pairs):
- 首先定义CONS过程的一种实现:
(define (cons a b) (lamdba (pick) (cond ((= pick 1) a) ((= pick 2) b)))) (define (car x) (x 1)) (define (cdr x) (x 2)) - 对一个例子使用代换模型:
(car (cons 37 49)) ==>(car (lamdba (pick) (cond ((= pick 1) 37) ((= pick 2) 49)))) ==>((lamdba (pick) (cond ((= pick 1) 37) ((= pick 2) 49)) 1) 1) ==>(cond((= 1 1) 37) ((= 1 2) 49)) ==>37
当时看到这里的时候,真的是深深被Lisp的数据和过程的理念所折服了,我们真的是从虚无中创造了数据,我们从纯过程的代换模型中成功的得到了pair的值,amazing!
抽象屏障
在我们实现每一层的数据抽象的时候,我们应该使其形成一层屏障,也就是要保证对于这一层级的数据的操作都被封锁在这一层中,不能向上也不能向下扩散,对外只能提供select和construct的接口.
在课程中教授也说到这可以视作是控制去中心化的思想,也就是每一层都来管理自己的东西,没有一个总的控制或者调度数据的地方.主要的优势是:
- 屏蔽了每个抽象数据类型的计算细节
- 对外提供的统一的接口可供调用
- 抽象不仅可以做水平的,也可以做每一层中不同实现的抽象,方便不同的实现方法.
消息传递vs.数据导向
这里主要讲到的是消息传递这种方式,但是结合后面的数据导向不免要做一番比较就写在这里了吧.
- 消息传递举了一种消息传递例子是:基于类型的派分.个人的感觉是消息传递就是给出一张信息表,每次调用的时候都去查表找到对应的操作交由它来完成功能并且返回结果.例子中讲到基于类型的派分也就是这样了(面向对象中常用的方法).缺陷是每次新加入表的一列(操作),之前的每一个类型都需要修改代码来实现这个操作,阻碍了系统拓展的灵活性.
- 数据导向数据导向更像是做出一个足够强大的类型,能够使其适应各种可能的操作,然后把它们组装在一起,在后面的例子通用运算包中也就是抽象了各种运算符(我觉得主要也是因为FP的特性,使得这种抽象很容易做到所以数据导向才会是一种更好的方式),然后只要将其组装在一起就可以了,在新增类型的时候,只要把类型和对应的操作实现,就可以直接”安装”在原有的系统中,而且原有的系统不需要修改一行代码就可以适应这种变化(课程中说到这是”免费”获得新的能力).
分层数据及其闭包性质
主要是讲了怎么使用闭包的性质来制造一些常用的数据结构(数据的组织和对应的操作方法).主要包括:
- Sequence(序列)
- List,Mapping list
- Tree(包括遍历和叶子节点概念),Mapping tree
用序列来连接传统的方法
主要是讲了怎么用模块连接的方式来解决问题.举例是遍历树的为奇数值的节点并且求平方之和和偶数的Fibnacci序列,在传统我们解决这类问题的时候都是把判断,筛选,组织结果的东西都放在一起,因为这样效率更高,但是一旦需求改变,这样的地方就需要全部重写,不仅拓展性差而且也不可复用.所以书中提到了流处理这种方式,就是把数据看做是流动的,从一系列的模块中数据流过去,自然而且就被过滤,选择并且获得了结果.
Ex.1:为奇数的树节点求和平方
- 枚举每一个节点
- 过滤,选择其中的奇数的节点
- 对2的所有数字分别平方
- 从0开始累积结果(求和)
Ex.2:偶数Fibnacci
- 从0开始枚举n
- 计算每一个n的Fibnacci值
- 过滤,选择其中的偶数
- 从0开始累积结果(求和)
我们可以看到这2个过程之间是有很多的相同的地方的,如果可以提取的话就可以复用而且增加拓展性.书中给出的抽象的方法就是流处理.大致的过程是:
- 产生数据的数据源
- 中间使用的各种过滤方法
- 最后对产生的结果进行累积的方法
可以发现经过这样的抽象之后,我们可以很轻松的拓展和修改上面的两个例子.比如:把过滤奇数的节点换成过滤偶数的,或者任意的规则,在累积结果时,也可以选择各种策略.相比把代码聚拢在一块里面的处理方式来说,将过程拆分开,变成处理数据流的方式确实更好.流处理数据的方式现在也被更多的语言和技术看重,Java甚至也可以直接使用streaming了.
例子:一个图形语言
主要就是使用前面讲到的类型的抽象和屏障对递归式的生成图片的方法进行了抽象

感觉还是十分的有趣的,可能是因为(人类的本质是复读机吧),还是挺喜欢看这种重复的图案构成花纹的感觉的.
符号语言
主要是讲了Lisp中的‘引用,举了使用引用来实现一个简单的微积分系统的例子和SET集合的例子.(引用主要是解决了一个哲学问题,就是用来区分引用和直接使用,从这里延伸下去又是一场哲学的战斗).
Huffman编码树
Huffman树感觉是这一节比较重要的例子就单独拿来出来,可以看到第二章还是贯穿了很多的数据结构的东西在里面的.
还是盗一张图吧,懒得自己搞图床了:)
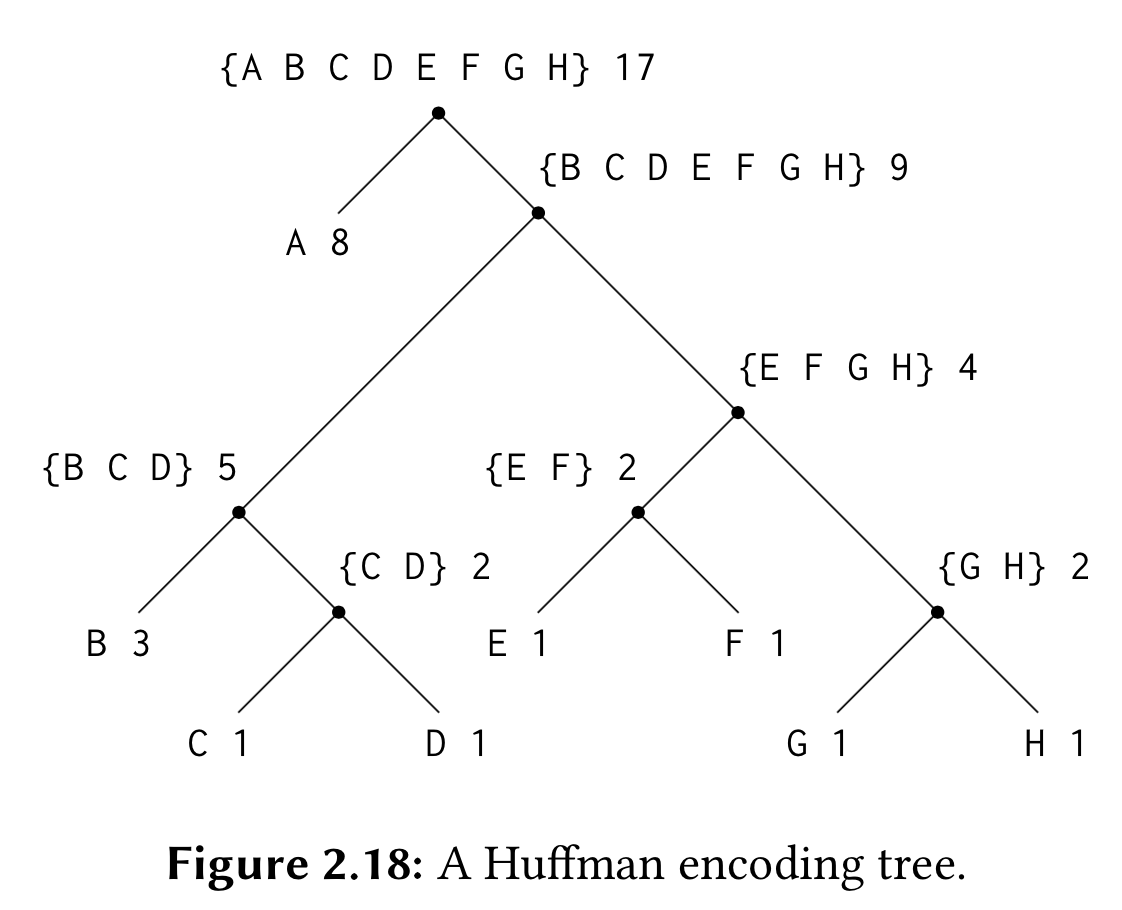
在看Huffman编码树的时候又去看了一遍刘末鹏的知其所以然(三):为什么算法这么难?,也是有了更深的理解(打算做一个总结,不过还没想好怎么写).
抽象数据的多重表示
主要还是举例子,复数的表示及其运算的表示,主要的思想在于结合了使用直角坐标系和极坐标系各自的优势,可以使得在处理复数的时候发挥不同的实现方式各自的优势,也就是之前提到过的抽象层中的竖直抽象层.
数据导向编程和可加性
主要还是对复数包功能的拓展和对数据导向编程和消息传递的比较.下面给出一个总结:
- 显式分派: 这种策略在增加新操作时需要使用者避免命名冲突,而且每当增加新类型时,所有通用操作都需要做相应的改动,这种策略不具有可加性,因此无论是增加新操作还是增加新类型,这种策略都不适合.
- 数据导向:数据导向可以很方便地通过包机制增加新类型和新的通用操作,因此无论是增加新类型还是增加新操作,这种策略都很适合.
- 消息传递:消息传递将数据对象和数据对象所需的操作整合在一起,因此它可以很方便地增加新类型,但是这种策略不适合增加新操作,因为每次为某个数据对象增加新操作之后,这个数据对象已有的实例全部都要重新实例化才能使用新操作.
通用的算术运算包
继续盗图:
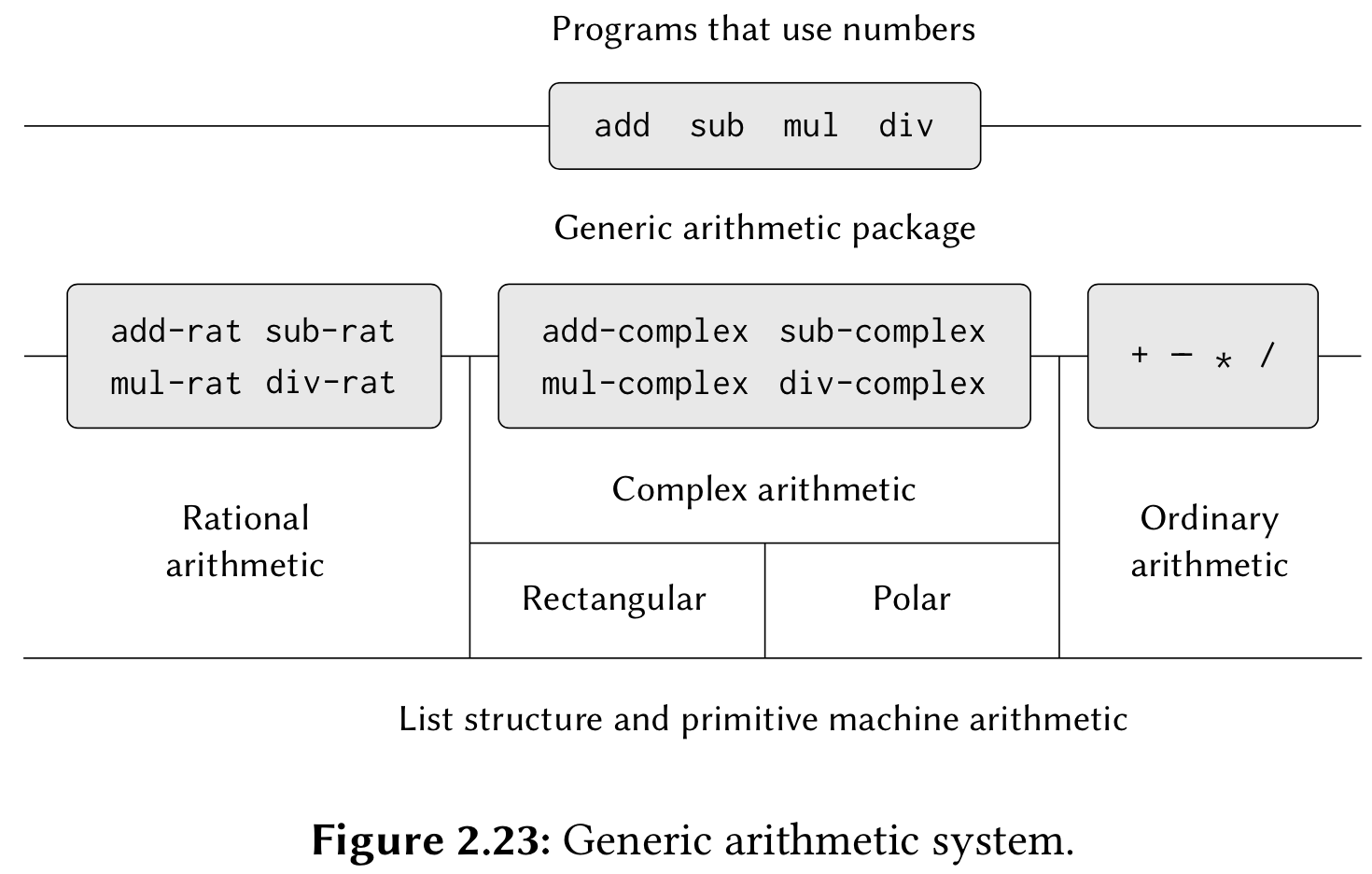
核心在于各种的抽象,抽象操作,抽象类型,做成分层的.当时看视频印象最深刻的就是当教授说当我们把所有的计算中的+-*/都换成抽象过程的时候,我们就可以免费的获得强大的拓展能力的时候,真的是_感觉很炫酷_,又_令人印象深刻_:不仅可以直接处理多项式的加法,而且多项式支持前面所有以及包含的有理数,复数,自然数的操作.由于多项式将自己注册入表中,我们甚至可以直接处理多项式的多项式.
总结
第二章的阅读进度不是很如意,感觉还是太拖沓了一点(TI看比赛也耽误了一个双休),总的来说第二章还是以大量的例子和习题为主,虽然感觉贯穿的知识点就那么几个,但是综合在一起之后所表现出来的强大的能力还是很令人震撼的,最起码可以实现一个简易的计算器了吧.感觉实习之后确实时间的分配不像学校那么的轻松了,但是能够每天还有自学的时间还算是很不错的了吧.
吾常终日而思矣,不如须臾之所学也.