MIT-CS6.00笔记Lec7-9

发表于 更新于 分类于

Lec7

Python数组:

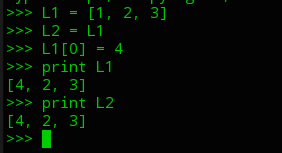
解释: L2 = L1 ==> 创建了一个L2和L1进行绑定,事实是L1和L2绑定了同一个对象,所以在通过L1改变了该对象的时候,L2也会发生变化,其实不是L1,L2的变化而是他们共同绑定的对象的变化.
Dictionaries(字典):

  • mutable
  • not ordered
  • generalized indexing

Pseudo code(伪代码):利用伪代码来控制程序流,拆分模块以及搞清对数据的操作

模块性和封装:不需要关心内部的具体实现,只需要调用就可以

efficiency-orders of growth(算法复杂度,运行效率):

  • 为什么我们需要考虑效率:因为问题的复杂度的增长速度远比计算机的发展更快
  • choice of algorithm:在遇到问题时,能够选择现有的算法并使得解决问题的效率加快
  • map problem into class of algorithm:将问题映射到一类算法

Space & Time:

  • how much memory to complete
  • what is it of basic steps needed as a function of the input size

Random access model:假定我们在读取任意一块内存区域的时候花费的时间是恒定的(理想状态)

  • best case -> Min
  • worst case -> Max
  • expected case -> Avg

Lec8

例子 整数a的b次幂的计算:

Iterative exponent: 

1
2
3
4
5
6
def exp1(a,b):    
    ans = 1    
    while (b>0):        
        ans += a        
        b -= 1    
    return ans

总共进行了2+3b步
O(b) -> liner

复杂度增长:

  • Asymototic notation
  • Big O notation - upper limit to growth

Recursive exponent: 

1
2
3
4
5
def exp2(a,b):    
    if b == 1:        
        return a    
    else:        
        return a*exp2(a,b-1)

分析递归式程序的复杂度: 

1
2
3
4
t(b) = 3 + t(b-1)     
     = 3 + 3 + t(b-2)     
     = 3*k + t(b-k)     
     Done b-k = 1

==> O(b)

二分: 

1
2
a ** b = (a*a) ** (b/2) -> b even       
       = a*(a**(b-1)) -> b odd
1
2
3
4
5
6
7
def exp3(a,b):    
    if b == 1:        
        return a    
    if (b%2)*2 == b:        
        return exp3(a*a, b/2)    
    else:        
        return a*exp3(a,b-1)

==> O(log b) 

1
2
3
4
5
b even t(b) = 6+t(b/2)
b odd  t(b) = 6+t(b-1)    
     ==>t(b) = 12 + t(b/2)            
             = 12k + t(b/2**k)        
    k = log2(b)

汉诺塔:

  • 经典的递归
  • O(2**n) -> 指数爆炸

Lec9

二分查找算法:
思想:

  • 1.确定first, last, mid=(first+last)/2
  • 2.判断如果mid是要找的值==>找到,否==>小于找左边,大于找右边
  • 3.mid=first || mid=last goto 1

缺点: 列表(list)不能用二分查找(效率低,复杂度变成线性复杂度)

Generalize:

  1. pick the mind point
  2. check to see if this is answer
  3. if not, reduce to smaller problem.Repeat

Question:

  • should we sort before search? ==>
    liner search n || sort & search nlogn+logn
  • can we sort in sub-liner time? - No
  • how fast can we sort? — nlogn

Amortize the cost:(平摊花费),如果只搜索一次的话,liner search效率更高,如果搜索多次的话,那么先排序就会体现优势在平摊了排序的花费,而查找的效率是logn.

排序算法

  • 选择排序 循环不变量:数组被分成2部分,pre和suff,前部分在排序中是有序的部分,每次只对后部分进行排序到有序为止.
  • 冒泡排序